ABCD is a quadrilateral in which P,Q,R and S are the mid points of sides AB,BC,CD and DA respectively AC is a diagonal
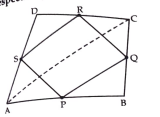
show that: PQ=SRSolution in Punjabi
Step by step video & image solution for ABCD is a quadrilateral in which P,Q,R and S are the mid points of sides AB,BC,CD and DA respectively AC is a diagonalshow that: PQ=SR by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Three angles of a quadrilteral are respectively 50∘ and 110∘ and 100∘ . Find the fourth angles.
View SolutionDefine a trial.
View SolutionDefine
Statistics as a subject.
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionIn the given figure, PQRS is a parallelogram. A and B are the mid-point of ¯¯¯¯¯¯PQ and ¯¯¯¯¯SR respectively. If PS=BR, then the quadrilateral ADBC is a…………………… ,
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E05_020_Q01.png" width="80%"gt
View SolutionABCD is a quadrilateral in which P, Q, R and S are mid- points of the sides AB, BC, CD and DA. AC is a diagonal. Show that :
PQ=SR
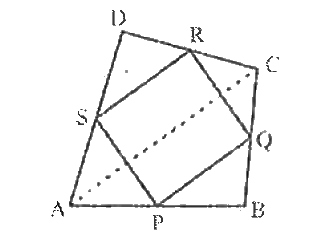
View SolutionABCD is a quadrilateral in which P, Q, R and S are mid- points of the sides AB, BC, CD and DA. AC is a diagonal. Show that :
PQRS is a parallelogram.
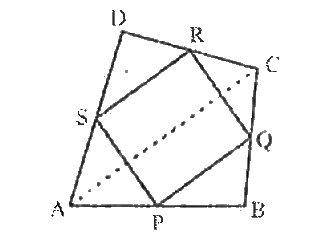
View SolutionABCD is a quadrilateral in which P,Q,R and S are mid points of the sides AB,BC,CD and DA. AC is a diagonal Show that:
SR∣∣ACandSR=12AC
PQ=SR
PQRS is a parallelogram
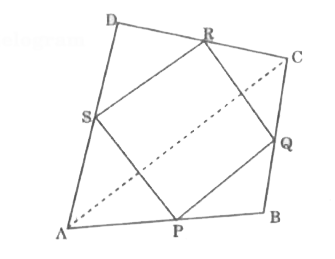
View SolutionIn quadrilateral ABCD if P,Q,R,S are mid-point of AB,BC,CD,DA resp. then SR is parallel to
View SolutionABCD is a quadrilateral in which P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively (See Fig.
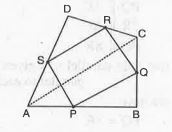 AC is a diagonal Show that SRIIACandSR=12AC.
AC is a diagonal Show that SRIIACandSR=12AC.
View Solution
