D is the midpoint of line segment AB. The co-ordinates of A and D are (2, 4) and (-1, 3), respectively. The co-ordinates of B are:

(-4, 2)

(-5, 4)

(4, -5)

(3, 1)

Video Solution

Text Solution

Generated By DoubtnutGPT

To find the coordinates of point B given that D is the midpoint of line segment AB, we can use the midpoint formula. The coordinates of A are (2, 4) and the coordinates of D are (-1, 3). We need to find the coordinates of B, which we will denote as (x2, y2).
1. Understand the Midpoint Formula: The midpoint D of a line segment AB is given by the formula:
$D = (\frac{x 1 + x 2}{2}, \frac{y 1 + y 2}{2})$
where (x1, y1) are the coordinates of point A and (x2, y2) are the coordinates of point B.
2. Identify the Coordinates:
- Coordinates of A (x1, y1) = (2, 4)
- Coordinates of D (x, y) = (-1, 3)
3. Set Up the Equations: From the midpoint formula, we can set up two equations based on the x-coordinates and y-coordinates:
- For the x-coordinates:
$\frac{2 + x 2}{2} = - 1$
- For the y-coordinates:
$\frac{4 + y 2}{2} = 3$
4. Solve for x2:
- Multiply both sides of the x-coordinate equation by 2:
$2 + x 2 = - 2$
- Subtract 2 from both sides:
$x 2 = - 2 - 2 = - 4$
5. Solve for y2:
- Multiply both sides of the y-coordinate equation by 2:
$4 + y 2 = 6$
- Subtract 4 from both sides:
$y 2 = 6 - 4 = 2$
6. Combine the Results: Now that we have both x2 and y2, we can write the coordinates of point B:
$B = (x 2, y 2) = (- 4, 2)$
Final Answer:
The coordinates of point B are (-4, 2).

Point P is the midpoint of segment AB. Co- ordinates of point P are (2,1) and that of point A are (11,5) . The co-ordinates of point B are
A $(- 7, - 3)$
B(6,5,3)
C(7,3)
D(-6, 5, -3)
The mid-point of the line-segment AB is P(0,4). If the coordinates of B are (-2, 3) then the co-ordinates of A are
A(2,5)
B3
C $\frac{13}{2}$
D $- \frac{13}{2}$
In the figure P(3, 2) is the mid-point of the line segment AB. What are the co-ordinates of A and B respectively:

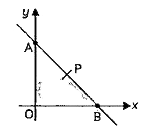A(4,0) and (6, 0)
B(0,4) and (6,0)
C(0,4) and (0,6)
D(0,-4) and (-6, 0)