What is the focal length of double concave lens kept in air with two spherical surfaces of radii R1=30cm and R2=60cm. Take refractive index of lens as n = 1.5.
From the figure using sign convention we get
R1=−30cm,R2=60cm and also given that n = 1.5
using 1/f=(n−1)(1/R1–1/R2)
1/f=(1.5−1)[1/(−30)−1/60]
Solving this, we get
Here minus indicates that the lens is divergent.

Topper's Solved these Questions
- REFRACTION OF LIGHT AT CURVED SURFACESBOOK - NCERT TELUGUCHAPTER - REFRACTION OF LIGHT AT CURVED SURFACESEXERCISE - Improve your learning (Application of concepts)
3 Videos
- REFRACTION OF LIGHT AT CURVED SURFACESBOOK - NCERT TELUGUCHAPTER - REFRACTION OF LIGHT AT CURVED SURFACESEXERCISE - IMPROVE YOUR LEARNING
3 Videos
- REFLECTION OF LIGHT BY DIFFERENT SURFACESBOOK - NCERT TELUGUCHAPTER - REFLECTION OF LIGHT BY DIFFERENT SURFACESEXERCISE - EXAMPLE
1 Videos
- REFRACTON OF LIGHT AT PLANE SURFACESBOOK - NCERT TELUGUCHAPTER - REFRACTON OF LIGHT AT PLANE SURFACESEXERCISE - IMPROVE YOUR LEARNING
6 Videos
Similar Questions
Knowledge Check
A lens has one concave surface of R1 = 2 m and convex surface with R2 = 3 m then focal length of lens is(if refractive index of the lens is 3/2)
A12 mB−12mC24D−6m
Find the focal length of a double-convex lens with R1=15cm and R2=−25CM. The refractivwe index of the lens mateirla n=1.5
View SolutionCalculate the focal length of a convex lens whose radii of curvature of two surfaces is 10cm and 15cm respectively and its refractive index is 1.5.
View SolutionCalculate the focal length of a biconvex lens in air if the radii of its surfaces are 60 cm and 15 cm. Refractive index of glass = 1.5
View SolutionCalculate the focal length of a biconvex lens in air if the radii of its surfaces are 60 cm and 15 cm. Refractive index of glass = 1.5
View SolutionA biconvex lens made of glass (refractive index 1.5) has two spherical surfaces having radii 20cm and 30cm. Calculate its focal length.
View SolutionA biconvex lens separates two media of refractive indices 1.3 and 1.7. the refractive index of the lens is 1.5 and the radii of curvature of the two sides of the lens are r1=10cm and r2=60cm .
The medium of refractive index 1.3 extends to 78 cm from the lens and that of refractive index 1.7 extends of 34 cm from the lens. A luminous object O is at a distance of 144 cm from the lens. Find the position of the final image from the lens.
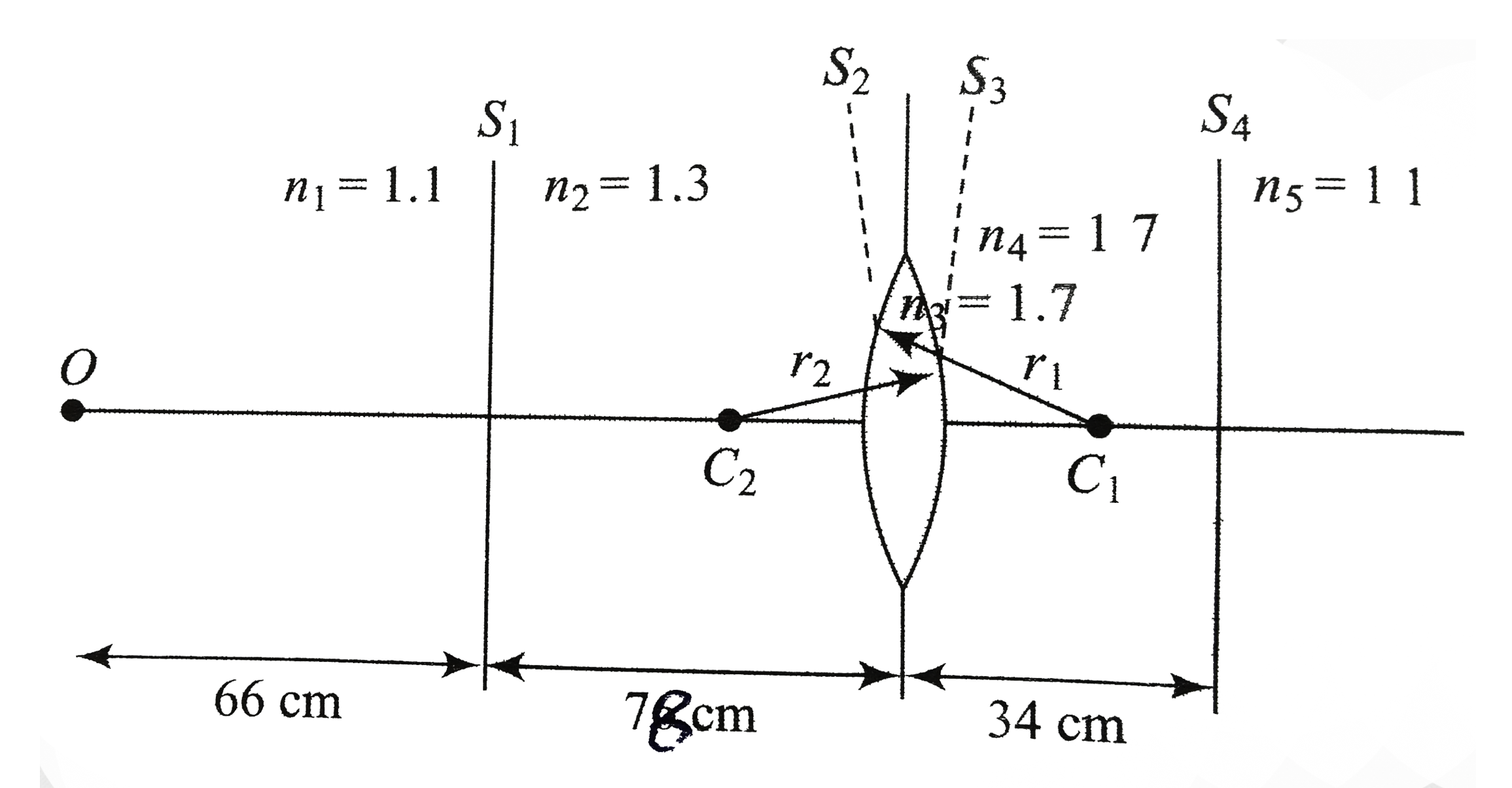
View SolutionA biconvex lens separates two media of refractive indices 1.3 and 1.7. the refractive index of the lens is 1.5 and the radii of curvature of the two sides of the lens are r1=10cm and r2=60cm .
The medium of refractive index 1.3 extends to 78 cm from the lens and that of refractive index 1.7 extends of 34 cm from the lens. A luminous object O is at a distance of 144 cm from the lens. Find the position of the final image from the lens.

View Solution
