What will be the number of the zero (s), if the graph of a quadratic polynomial does not intersect the x-axis ?
zero
one
two
three
The correct Answer is:A
Topper's Solved these Questions
- SAMPLE PAPER 6BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - SECTION C
10 Videos
- SAMPLE PAPER 6BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - SECTION- A
20 Videos
- SAMPLE PAPER 6BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - SECTION- C
10 Videos
- SAMPLE PAPER 5BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - PART - B (SECTION - V)
4 Videos
- SAMPLE PAPER 7BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - PART - B (SECTION - V)
8 Videos
Similar Questions
Knowledge Check
Which of the following is not the graph of a quadratic polynomial?
A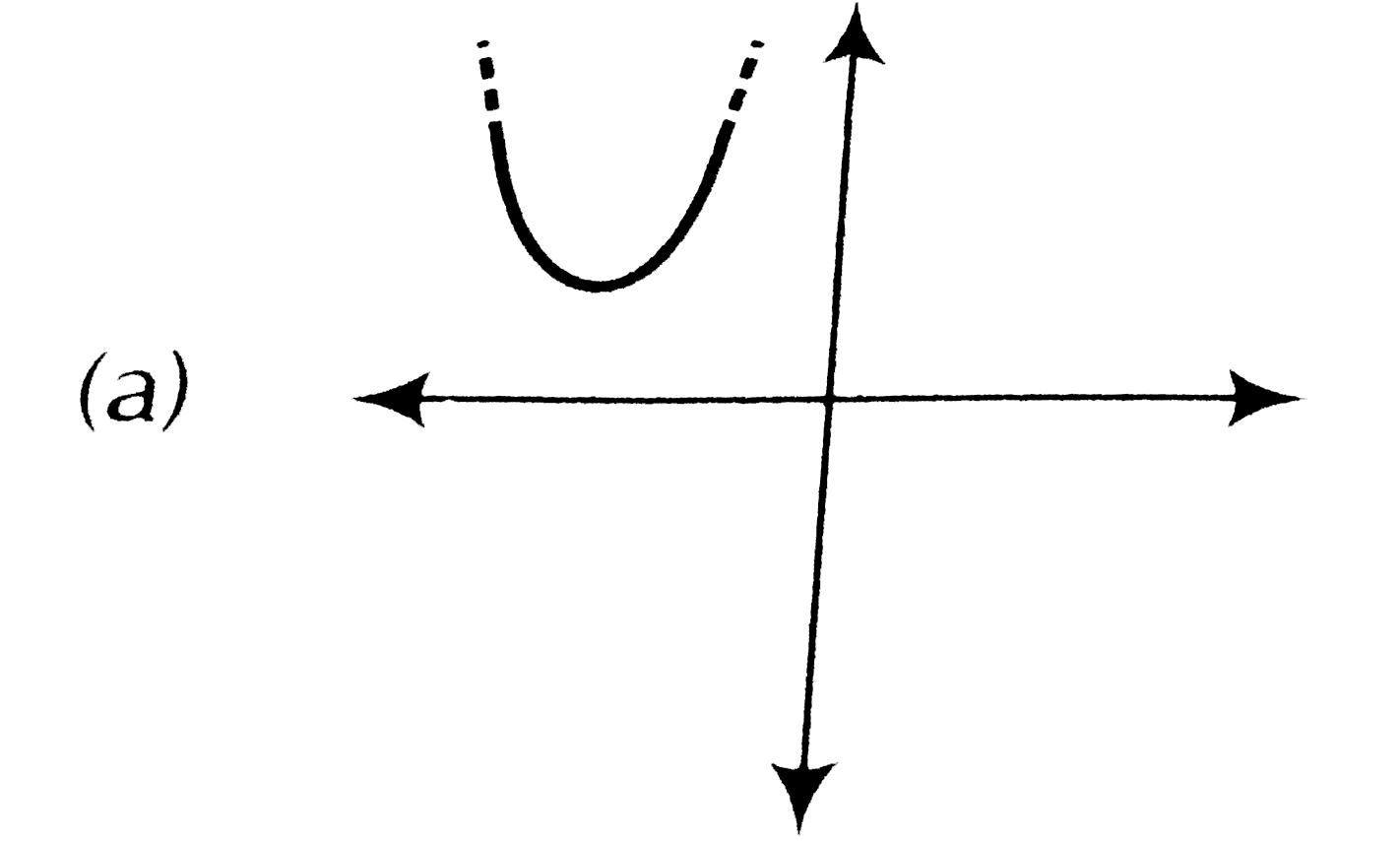 B
B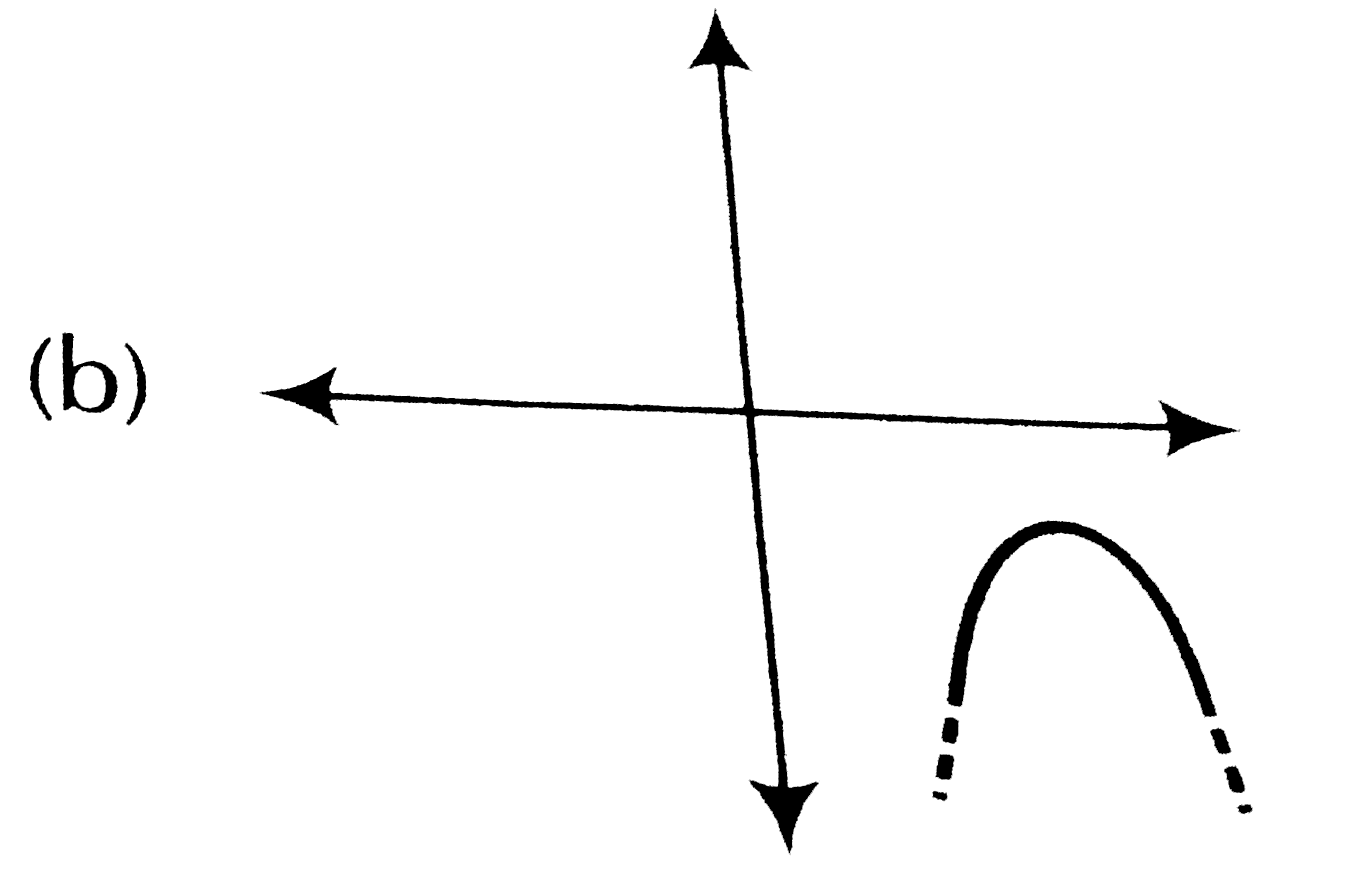 C
C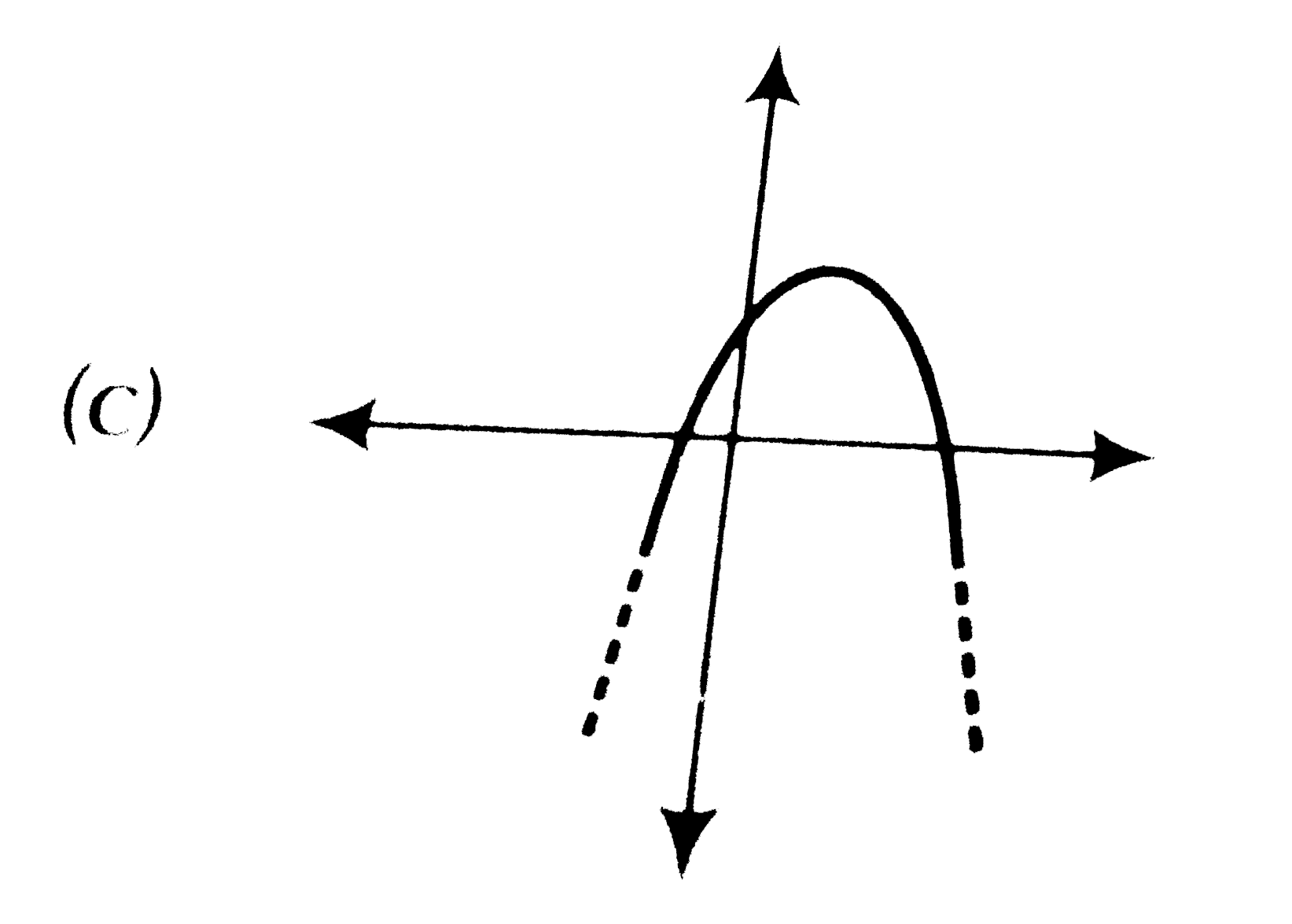 D
D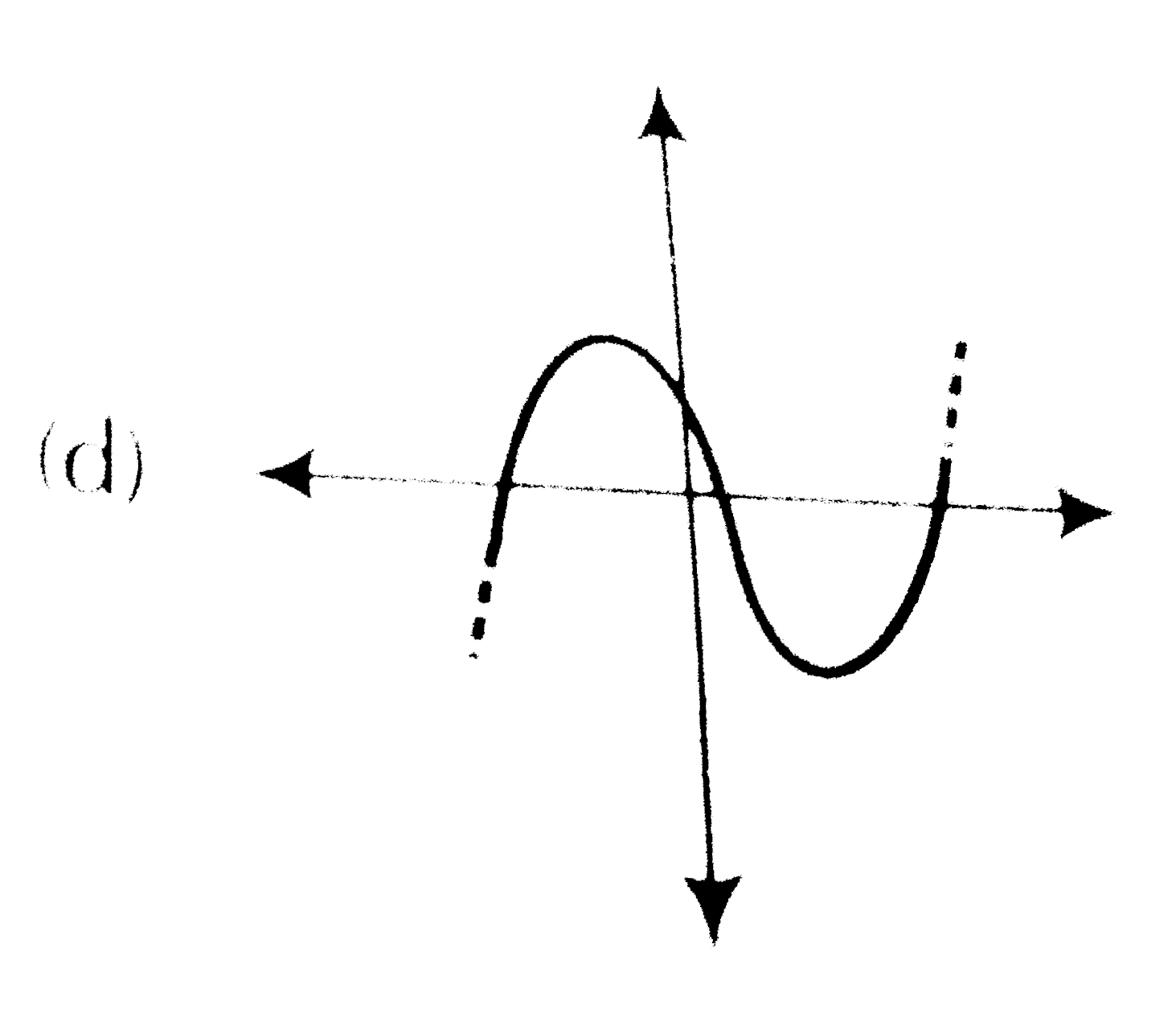
Assertion (A) : The zeroes of the polynomial p(x)=(x−1)(x−2)(x−3) are 1,2 and 3
Reason (R):The zeroes of a polynomial are the x-coordinates of the points where the graph of polynomial intersects or touches x-axis or the points on the graph where p(x)=0ABoth A and R are true and R is the correct explanation for aBBoth A and R are true and R is not correct explanation for A.CA is true but R is false.DA is false but R is true
Calculate the number of zeroes for the graph of a polynomial p(x) as shown below:
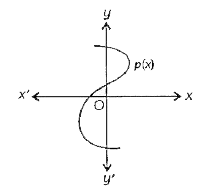
View SolutionWhat will be number of zeros of the polynomials whose graphs are either touching or intersecting the axis only at the points :
(i)(3,0), (0,2) & (3,0) (ii)(0,4), (0,0) and (0,−4)
View SolutionGraph of quadratic polynomial When polynomial have no zeroes
View SolutionAre the following statements 'True' or 'False'? Justify your answer.
(i) If the zeroes of a quadratic polynomial ax2+bx+c are both positive, then a,b and c all have the same sign.
(ii) If the graph of a polynomial intersects the X-axis at only one point, it cannot be a quadratic polynomial.
(iii) If the graph of a polynomial intersects the X-axis at exactly two points, it need not ve a quadratic polynomial.
(iv) If two of the zeroes of a cubic polynomial are zero, then it does not have linear and constant terms.
(v) If all the zeroes of a cubic polynomial are negative, then all the coefficients and the constant term of the polynomial have the same sign.
(vi) If all three zeroes of a cubic polynomial x3+ax2−bx+c are positive, then atleast one of a,b and c is non-negative.
(vii) The only value of k for which the quadratic polynomial kx2+x+k has equal zeroes is 12.
View SolutionWhat is the other zero of the polynomial, if one zero of the quadratic polynomial 2x2−8x−m is 52?
View SolutionAre the following statements True or False Justify your answers.
If the graph of a polynomial intersects the x- axis at only one point ,it cannot be a quadratic polynomial .
View Solution
