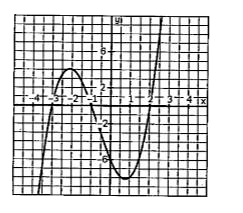
Find the zeroes of the curve.
−3,−6,−1
2,−6,−1
−3,−1,2
3,1,−2
The correct Answer is:C
Step by step video, text & image solution for Find the zeroes of the curve. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 1EXERCISE - Section -A20videos
SAMPLE PAPER 1
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 1EXERCISE - Section -B20videos
SAMPLE PAPER 1
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 1EXERCISE - SECTION B20videos
SAMPLE PAPER 1
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 07EXERCISE - SECTION -C10videos
SAMPLE PAPER 07
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 10EXERCISE - SECTION-C10videos
SAMPLE PAPER 10
Similar Questions
The tangents to a curve at a point on it is perpendicular to the line joining the point with the origin. Find the equation of the curve.
View SolutionThe tangents to a curve at a point on it is perpendicular to the line joining the point with the origin. Find the equation of the curve.
View Solution_______ helps in finding the areas of the curves.
View SolutionThe slope of tangent at a point P(x,y) on a curve is −xy. If the curve passes through the point (3, -4) , find the equation of the curve.
View SolutionThe slope of the tangent at a point P(x,y) on a curve is (−y+3x+2). If the curve passes through the origin, find the equation of the curve.
View SolutionA curve is such that the length of the polar radius of any point on the curve is equal to the length of the tangent drawn at this point. Form the differential equation and solve it to find the equation of the curve.
View SolutionThe slope of the tangent to the curve at any point is equal to y + 2x. Find the equation of the curve passing through the origin .
View SolutionFind the area under the curve
View SolutionFind the quadratic polynomial, the sum of whose zeros is (52) and their product is 1. Hence, find the zeros of the polynomial.
View SolutionFind the quadratic polynomial, the sum of whose zeros is √2 and their product is −12. Hence, find the zeros of the polynomial.
View Solution

