A projectile is thrown from a point O on the ground at an angle 450 from the vertical and with a speed 5√2ms. The projectile at highest point of its tracjectory splits into two equal parts. One part falls vertically down to the ground 0.5s after the splitting. The other part t seconds after the splitting falls to the ground at a distance x meters from the point O. The acceleration due to gravity g=10ms2. The value of x is
To solve the problem, we will break it down into several steps:
Step 1: Analyze the initial conditions
The projectile is thrown from point O at an angle of 45∘ from the vertical with a speed of 5√2m/s. Since the angle is given from the vertical, the angle from the horizontal is also 45∘.
Step 2: Resolve the initial velocity into components
The initial velocity u can be resolved into horizontal and vertical components:
- Horizontal component:
ux=usin(45∘)=5√2⋅1√2=5m/s
- Vertical component:
uy=ucos(45∘)=5√2⋅1√2=5m/s
Step 3: Determine the time to reach the highest point
At the highest point, the vertical component of the velocity becomes zero. The time th to reach the highest point can be calculated using:
th=uyg=510=0.5s
Step 4: Calculate the maximum height reached
The maximum height H can be calculated using the formula:
H=uyth−12gt2h
Substituting the values:
H=5⋅0.5−12⋅10⋅(0.5)2=2.5−1.25=1.25m
Step 5: Analyze the splitting of the projectile
At the highest point, the projectile splits into two equal parts. One part falls vertically down, taking 0.5s to reach the ground. The other part will have the same horizontal velocity ux=5m/s and will fall to the ground after t seconds.
Step 6: Calculate the time of flight for the second part
The time t for the second part to fall to the ground can be determined from the height H:
H=12gt2
Substituting the values:
1.25=12⋅10⋅t2
1.25=5t2⟹t2=0.25⟹t=0.5s
Step 7: Calculate the horizontal distance traveled by the second part
The horizontal distance x traveled by the second part during its time of flight t is given by:
x=ux⋅t=5⋅0.5=2.5m
Step 8: Calculate the total distance from point O
Since the first part fell vertically down and the second part traveled horizontally, the total distance x from point O is:
x=horizontal distance at highest point+horizontal distance traveled by second part
The horizontal distance at the highest point (before splitting) is:
Distance at highest point=ux⋅th=5⋅0.5=2.5m
Thus, the total distance x is:
x=2.5+2.5=5m
Final Answer
The value of x is 5m.
---
The projectile is thrown from point O at an angle of 45∘ from the vertical with a speed of 5√2m/s. Since the angle is given from the vertical, the angle from the horizontal is also 45∘.
The initial velocity u can be resolved into horizontal and vertical components:
- Horizontal component:
ux=usin(45∘)=5√2⋅1√2=5m/s
- Vertical component:
uy=ucos(45∘)=5√2⋅1√2=5m/s
At the highest point, the vertical component of the velocity becomes zero. The time th to reach the highest point can be calculated using:
th=uyg=510=0.5s
The maximum height H can be calculated using the formula:
H=uyth−12gt2h
Substituting the values:
H=5⋅0.5−12⋅10⋅(0.5)2=2.5−1.25=1.25m
At the highest point, the projectile splits into two equal parts. One part falls vertically down, taking 0.5s to reach the ground. The other part will have the same horizontal velocity ux=5m/s and will fall to the ground after t seconds.
The time t for the second part to fall to the ground can be determined from the height H:
H=12gt2
Substituting the values:
1.25=12⋅10⋅t2
1.25=5t2⟹t2=0.25⟹t=0.5s
The horizontal distance x traveled by the second part during its time of flight t is given by:
x=ux⋅t=5⋅0.5=2.5m
Since the first part fell vertically down and the second part traveled horizontally, the total distance x from point O is:
x=horizontal distance at highest point+horizontal distance traveled by second part
The horizontal distance at the highest point (before splitting) is:
Distance at highest point=ux⋅th=5⋅0.5=2.5m
Thus, the total distance x is:
x=2.5+2.5=5m
The value of x is 5m.
Topper's Solved these Questions
Similar Questions
Put a unifrom meter scale horizontally on your extended index fingers with the left one at 0.0 cm and the right one at 90.00 cm when you attempt to move both the fingers slowly towards the center , initially only the left finger slips with respect to to the scale and the right finger does not . after some distance, the left finger stops and the right one starts slipping . Then the right finger stops at a distance XR from the center (50.00 cm ) of the scale and the left one starts slopping again . This happens because to the difference in the fiictional forces on the two fingers . it the coefficients of static and dynamic between the fingers and the scale are 0.4 and 0.32 respectively , the value of XR (in cm is ...........
View SolutionA small circular loop of area A and resistance R is fixed on a horizontal xy -plane with the center of the loop always on the axis ˆn of a long solenoid . The solenoid has m turns per unit length and carries current I counterclockwise as shown in the figure . THe magnetic field due to the solenoid is in ˆn direction, List -I gives time dependences of ˆn in terms of a constant angular frequency ω , List - II gives the torques experienced by the circular loop at time t=π6ω Let α=A2μ20m2l2ω2R
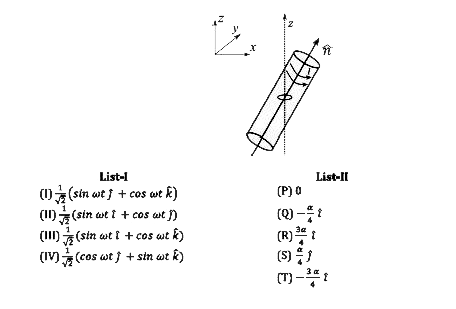
which one of the following options is correct ?
View SolutionA bomb is thrown at a speed 20m/s at an angle 45∘. At the highest point , it explodes into two parts of equal mass , the one part coming to rest. Find the distance from the origin to the point where the other part strikes the ground.
View SolutionA projectile of mass "m" is projected from ground1 with a speed of 50 m/s at an angle of 53∘ with the horizontal. It breaks up into two equal parts at the highest point of the trajectory. One particle coming to rest immediately after the explosion.
The distance between the pieces of the projectile when they reach the ground are :
View SolutionA projectile is moving at 60 m//s at its highest point, where it breaks into two equal parts due to an internal explosion. One part moves vertically up at 50m//s with respect to the ground. The other part will move at
View SolutionA projectile of mass 20 kg is fired with a velocity of 400m//s at an angle of 45^(@) with the horizontal .At the highest point of the trajectocy the projectile explodes into two fragments of equal mass,one of which falls vertically downward with zero initial speed, The distance of the point where the other fragment falls from the point offiring is:
View SolutionA projectile at its highest point, breaks into two equal parts due to an internal explosion. One part moves vertically up at 30 m/s with respect to ground. Then the other part will move with speed if (Speed just before explosion is 20 m/s) :
View SolutionA projectile is moving at 20 m s^(-1) at its highest point where it breaks into equal parts due to an internal explosion. Just after explosion, one part moves vertically up at 30 ms^(-1) with respect to the ground. Then the other part will move at :
View SolutionGround To Ground Projectile | Part 2
View SolutionThe vertical and horizontal displacements of a projectile thrown from a point on the ground at time t are given by y=6t-5t^(2) and x=8t respectively,where x and y are in meters and t is in seconds.The time of flight of the projectile in seconds is ?
View SolutionA projectile of mass M is fired so that the horizontal range is 4 km. At the highest point the projectile explodes in two parts of masses M/4 and 3M/4 respectively and the heavier part starts falling down vertically with zero initial speed. The horizontal range (distance from point of firing) of the lighter part is:
View SolutionA projectile of mass M is fired so that the horizontal range is 4 km. At the highest point the projectile explodes in two parts of masses M/4 and 3M/4 respectively and the heavier part starts falling down vertically with zero initial speed. The horizontal range (distance form point of fring) of the lighter part is :
View SolutionA projectile of mass M is fired so that the horizontal range is 4 km. At the highest point the projectile explodes in two parts of masses M/4 and 3M/4 respectively and the heavier part starts falling down vertically with zero initial speed. The horizontal range (distance form point of fring) of the lighter part is :
View SolutionA projectile of mass M is fired so that the horizontal range is 4 km. At the highest point the projectile explodes in two parts of masses M/4 and 3M/4 respectively and the heavier part starts falling down vertically with zero initial speed. The horizontal range (distance form point of fring) of the lighter part is :
View SolutionAt an initial speed of 50 m / s, a particle of 24 kg moves horizontally upwards 53^(@) Who is projected on. The projectile at the highest point of the path splits into two parts of equal mass. The first particle falls vertically downward at zero initial velocity. How far will the second particle hit the ground from the projectile point? (Suppose the ground surface is flat.) (b) How much energy will be free during partition?
View SolutionA projectile is thrown from the ground with a speed of 2sqrtgh at an angle of 60^@ to the horizontal from a point on the horizontal ground . The horizontal range of the projectile is
View Solution
