A ray of light falls on a plane mirror at angle of $35^{\circ}$ . The value of $θ$ is

A

$35^{\circ}$

B

$45^{\circ}$

C

$55^{\circ}$

D

$90^{\circ}$

Text Solution

Verified by Experts

The correct Answer is:A

According to the question,

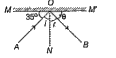
From figure, $∠ M O A + ∠ A O N = 90^{\circ}$
$35^{\circ} + ∠ A O N = 90^{\circ}$
$∠ A O N = 90^{\circ} - 35^{\circ} = 55^{\circ}$
According to the law of reflection, $∠ i = ∠ r = ∠ A O N = 55^{\circ}$
Since, $∠ N O B + ∠ B O M . = 90^{\circ}$
$55^{\circ} + ∠ B O M . = 90^{\circ}$
$∠ B O M . = 90^{\circ} - 55^{\circ} + 35^{\circ}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Similar Questions

Knowledge Check

Question 1 - Select One
A ray of light on a plane mirror at an angle of $60^{\circ}$ . What is the deviation produced by the mirror ?
A $120^{\circ}$
B $60^{\circ}$
C $30^{\circ}$
D $90^{\circ}$
Question 2 - Select One
A ray of light incident on a plane mirror at angle $θ$ . If the angle between the incident and reflected rays is $80^{\circ}$ , what is the value of $θ$
A $40^{\circ}$
B $50^{\circ}$
C $45^{\circ}$
D $55^{\circ}$
Question 3 - Select One
When a ray of light strikes a plane mirror at an angle of $15^{\circ}$ with the mirror, what will be the angle through which the ray gets deviated?

A $15^{\circ}$
B $30^{\circ}$
C $75^{\circ}$
Dnone of these

Recommended Questions

Home
Ask Doubt
Profile