If magnification m=+1.5 , then
size of the lmage = size of the object real image
size of the image > size of the object , real image
size of the object > size of the image , virtual image
size of the object is twice the size of the image , virtual image .
The correct Answer is:B
Magnification .
(m)=Size of image (l)Size of object (O)
1.5=lO
32=lO
∴ l=32O
i.e., Size of the image > Size of the object .
Since m, is positive , hence image is real .
Similar Questions
A telescope with magnification M = 15 was submerged in water so that the inside of the telescope is filled up with water. To make the system work as a telescope within the former dimensions, the objective was removed. What was the magnification of the telescope after the change? μ of the material of the eye-piece=1.5 and μ of water =43
View SolutionWhen an object is placed at a distance of 25 cm from a mirror, the magnification is m1. The object is moved 15 cm further away with respect to the earlier position, and the magnification becomes m2. If m1/m2=4, the focal length of the mirror is
View Solution
Knowledge Check
When an object is placed at a distance of 25 cm from a mirror, the magnification is m1 . But the magnification becomes my, when the object is moved 15 cm farther away with respect to the earlier position. If m1m2 =4 then find the focal length of the mirror and what type of mirror it is?
A20 cm, convexB20 cm, concaveC10 cm, convexD10 cm, concaveThe formula for magnification m of a lens is :
AvuB−vuCuvD−uvThe focal length of objective and eye-piece of a compound microscope are 1 cm and 5 cm respectively. The microscope magnification is equal to 50. If the distance between two lenses is increased by 2 cm then the magnification is
A31B60C16D83
When an object is placed at a distance of 25 cm from a mirror, the magnification is m1. The object is moved 15cm farther away with respect to the earlier position, and the magnification becomes m2. If m1/m2=4 , then calculate the focal length of the mirror.
View SolutionWhen an object is placed at a distance of 25 cm from a mirror, the magnification is m1. The object is moved 15cm farther away with respect to the earlier position, and the magnification becomes m2. If m1/m2=4 , then calculate the focal length of the mirror.
View SolutionConsider a concave mirror and a convex lens (refractive index 1.5) of focal length 10cm each separated by a distance of 50cm in air (refractive index = 1) as shown in the Fig. An object is placed at a distance of 15cm from the mirror. Its erect image formed by this combination has magnification M1. When this set up is kept in a medium of refractive index 7/6, the magnification becomes M2. The magnitude (M2M1) is :
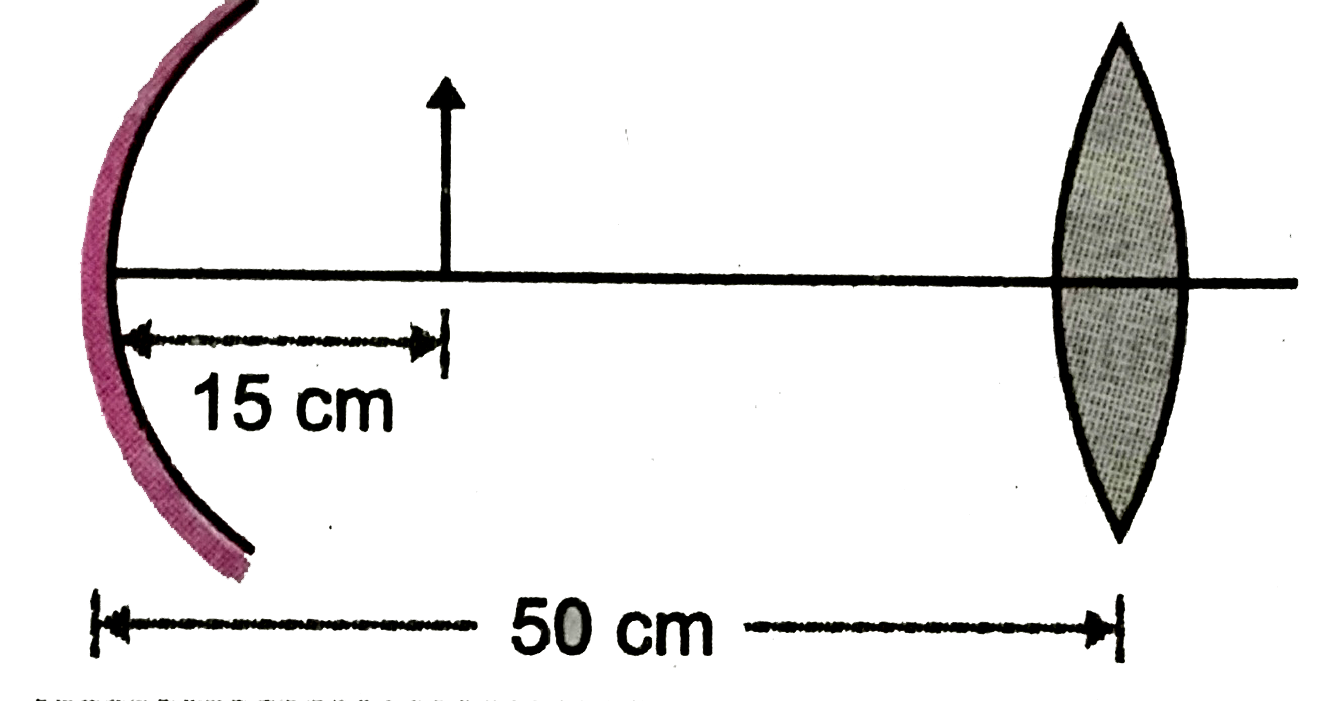 .
.
View SolutionIf the magnification of a body of size 1 m is 2, what is the size of the image ?
View SolutionConsider a concave mirror and a convex lens (refractive index 1.5) of focal length 10cm each separated by a distance of 50cm in air (refractive index = 1) as shown in the Fig. An object is placed at a distance of 15cm from the mirror. Its erect image formed by this combination has magnification M1. When this set up is kept in a medium of refractive index 7/6, the magnification becomes M2. The magnitude (M2M1) is :
 .
.
View Solution
