The size of the image formed by a convex mirror when an object is placed at infinity is

A

point sized

B

enlarged

C

large

D

same size

Text Solution
Verified by Experts

The correct Answer is:A

The size of Image formed by a convex mirror when an object is placed at Infinity is point sized. Image by convex mirror in this case will be
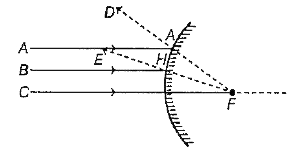
ocr_image
So, the image will be formed at focal point and a point size.

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 12PHYSICSSOLVED PAPER 2019

Similar Questions

Knowledge Check

  • The image formed by a convex mirror of a real object is

    Avirtual and erect
    Bvirtual and inverted
    Creal and erect
    Dreal and inverted

  • What will be the size of the image formed by a concave mirror when an object placed between Pole and Focus?

    ASame Size
    BEnlarged
    CPoint Size
    DDiminished

  • What will be the size of image formed by a concave mirror when an object placed between Pole and Focus?

    ASame Size
    BDiminished
    CPoint Size
    DEnlarged