Ab Bc Cd De Ef Fg G?
A
i
B
H
C
I
D
h
Video Solution
Text Solution
The correct Answer is:D
The given sequence is a combination of small-cap letter that follows the pattern :

Therefore, missing letter=h.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - LUCENT PUBLICATIONCHAPTER - SERIES COMPLETION : ALPHABETEXERCISE - EXERCISE 249videos
SERIES COMPLETION : ALPHABET
- BOOK - LUCENT PUBLICATIONCHAPTER - SEQUENTIAL OUTPUT TRACINGEXERCISE - Exercise -45videos
SEQUENTIAL OUTPUT TRACING
- BOOK - LUCENT PUBLICATIONCHAPTER - SERIES COMPLETION : MIXED SERIESEXERCISE - Exercise ( Type-V: Miscellaneous )1videos
SERIES COMPLETION : MIXED SERIES
Similar Questions
Knowledge Check
- Question 1 - Select One
In ΔABCandΔDEF, we have ABDE=BCEF=ACDF=57, then ar(ΔABC):ar(ΔDFR)=?
A5:7B25:49C49:25D125:343 - Question 2 - Select One
In the given figure AB⊥BEandEF⊥BE. Also BC=DE and AB= EF. Then
 AΔABD≅ΔEFCBΔABD≅ΔEFCCΔABD≅ΔCMDDΔABD≅ΔCEF
AΔABD≅ΔEFCBΔABD≅ΔEFCCΔABD≅ΔCMDDΔABD≅ΔCEF - Question 3 - Select One
In ΔABCandΔDEF, it is given that AB = DE and BC = EF. In order that ΔABC≅ΔDEF, we must have
A∠A=∠DB∠B=∠EC∠C=∠FDnone of these
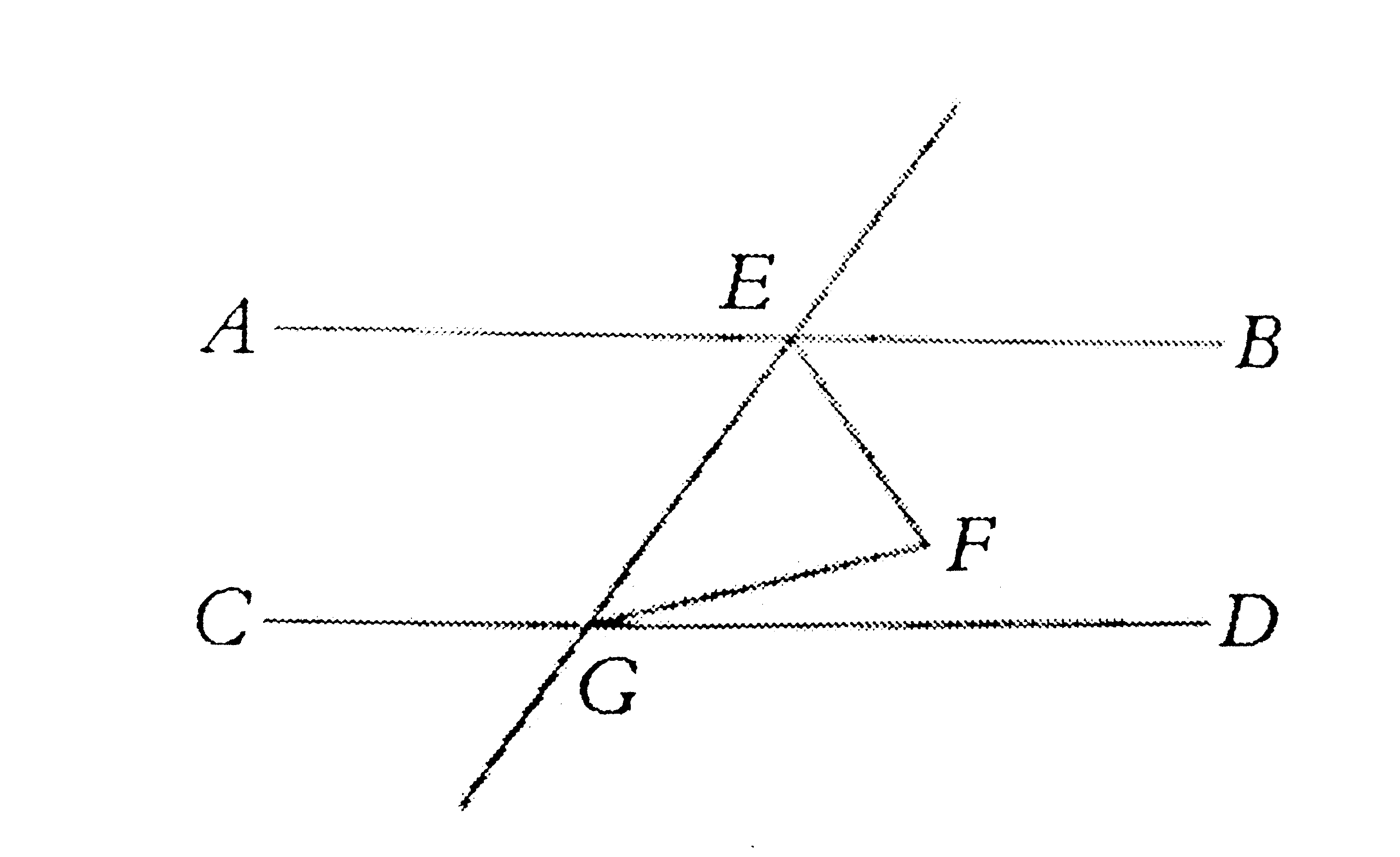
In the figure above, AB || CD. EF and FG are the bisectors of ∠BEGand∠DGE, respectively. ∠FEG=∠FGE+10∘. Find ∠FGE.View SolutionTwo triangles ΔABCandΔDEF are given such that AB||DE,BC||EFandAB=DE,BC=EF."Show that"AC"||"DFandAC=DE
View SolutionIf ΔABC~ΔDEFandAB=DE,BC=8cm, then the value of EF ?
View SolutionIn ΔABCand ΔDEF,AB=DEandBC=EF. Then one can infer that
ΔABC=ΔDEF, whenView SolutionΔABCandΔDEF are similar such that ABDE=BCEF. Area of the two triangles are respectively 16cm2and49cm2. If BC=2√2cm, then what is length of EF ?
View Solution