A group of 630 children is arranged in rows for a group photograph session. Each row contain three fewer children than the row in front of it. What number of rows is not possible ?
3
4
5
6
The correct Answer is:D
Let the number of rows = x, and the number of children in last row = y. Then, according to the question
xy+3(x−1)(x)2=630 ......(i)
So, check out all possibilities given in the options.
Put x=3 in equation (i), we get 3y+9=630
or y=207
So, it is possible.
Put x=4 in equation (i), we get 4y+18=630or, y=153
So, it is also possible.
Put x=5 in equation (i), we get 5y+30=630
or, y=120
So, it is also possible.
Put x=6 in equation (i), we get 6y+45=630
or, y=5856=97.5
So, it is not possible. [∵ No. of children can.t be in fraction]
Therefore, the number of rows not possible = 6
Topper's Solved these Questions
- MATHEMATICAL ABILITY AND REASONINGBOOK - LUCENT PUBLICATIONCHAPTER - MATHEMATICAL ABILITY AND REASONINGEXERCISE - EXERCISE (Type-I: Calculation Based Problems)
47 Videos
- MATHEMATICAL ABILITY AND REASONINGBOOK - LUCENT PUBLICATIONCHAPTER - MATHEMATICAL ABILITY AND REASONINGEXERCISE - EXERCISE (Type-II: Figure Based Problems)
5 Videos
- LOGICAL VENN DIAGRAMS BOOK - LUCENT PUBLICATIONCHAPTER - LOGICAL VENN DIAGRAMS EXERCISE - EXERCISE -4
3 Videos
- MATHEMATICAL OPERATIONS BOOK - LUCENT PUBLICATIONCHAPTER - MATHEMATICAL OPERATIONS EXERCISE - EXERCISE-3
34 Videos
Similar Questions
What would be the next row of the numbers ?
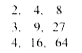
View SolutionIna class of 72 children are seated in rows and columns is such a way that the number of children in each row is 12.5% more than the number of children in each column. How many children are there in each row? 8 b. 9 c. 12 d. 18 e. none of these
View Solution
Knowledge Check
Ten players are to be seated in a row for photographs , so that the two particular players sit in the 2 middle seats. The number of arrangements is
A9!B(9!)(2!)C2.(8!)Dnone of theseIf there are x rows of chairs and each row contains 3x chairs. Determine the total number of chairs.
A3x2B2x3Cx2Dx3There are 24 peaches, 36 apricots and 60 bananas and they have to be arranged in several rows in such a way that every row contains the same number of fruits of only one type. What is the minimum number of rows required for this to happen
A12B9C10D6
The numbers of ways can 6 boys and 5 girls be arranged for a group photograph if the girls are to sit on chairs in row and the boys are to stand in a row behind them is
View SolutionIn how many ways can 6 boys and 5 girls be arranged for a group photograph if the girls are to sit on chairs in a row and the boys are to stand in a row behind them?
View SolutionThere is certain number of rows of chairs in a room .The number of chairs in each row is thrice the total number of rows. Find the number of charis in each row and number of rows in the room if the total number of chairs is 2187
View SolutionIf there are x rows of chairs and each row contains x2 chairs. Determine the total number of chairs.
View SolutionStudents of a class are made to stand in rows. If one student is extra in a row, there would be two rows less. If one student is less in a row, there would be three rows more. What is the number of students in the class ?
View Solution
