Doubtnut Promotions Sticky

Number of letters skipped in between adjacent letters in the series decreases by one each time.

A

BHNSV

B

IMTXB

C

MSYBG

D

TZEIL

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:D

The required pattern is as follows:
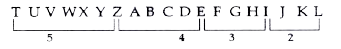
ocr_image
So, number of skipped letters decreases by one each time i.e. 5,5−1=4,4−1=3,3−1=2.

|
Updated on:21/07/2023
Class 14REASONINGALPHABET TEST : ALPHABET SERIES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    In the following question, num ber of letters skipped in between adjacent letters in the series decreases one each time. Which of the following series observes the rule?

    AMSYBG
    BIMTXB
    CBHNSV
    DTZEIL
  • Question 2 - Select One

    The number of letters skipped in between adjacent letters in the series is increased by one each time. Which of the following series observes the rule?

    AADHMS
    BHKOSV
    CGJNSX
    DFLQUX
  • Question 3 - Select One

    Number of letters skipped in be tween adjacent letters in the series increases by one every time. Which of the following series observes this rule?

    AACFKO
    BDGKPV
    CDBKAM
    DQSVXZ