The velocity of a transverse wave on a string of length 0.5m is 225m/s.
What is the fundamental frequency of a standing wave on this string if both ends are kept fixed ?
Text Solution
The wavelength of the fundamental mode is λ=2l. Hence the fundamental frequency is
n=v2l=225m/s2×0.5m=225s−1=225Hz. While the string is vibrating in the fundamental harmonic, the frequency of the sound produced by the string will be same as the fundamental frequency of the string. The wavelength of sound produced is =vsn=330m/s225s−1=1.67m
|
Similar Questions
Knowledge Check
If the speed of a transverse wave on a stretched string of length 1 m is 60ms−1, what is the fundamental frequency of vibration ?
A40 HzB45 HzC35 HzD30 HzThe velocity of waves in a string fixed at both ends is 3 m/s. The string forms standing waves with nodes 6 cm apart. The frequency of vibration of the string is
A25 HzB50 HzC15 HzD10 Hz
Standing Wave Vibrations of string fixed at both ends
View SolutionStanding Wave Equation||Transverse wave in a string
View SolutionWhat is maximum possible wavelength of standing waves in 1m long string if it is fixed at both ends
View SolutionWhat is maximum possible wavelength of standing waves in 1m long string if it is fixed at both ends
View SolutionFor a stationary wave set up in a string having both ends fixed, what is the ratio of the fundamental frequency to the third harmonic?
View Solution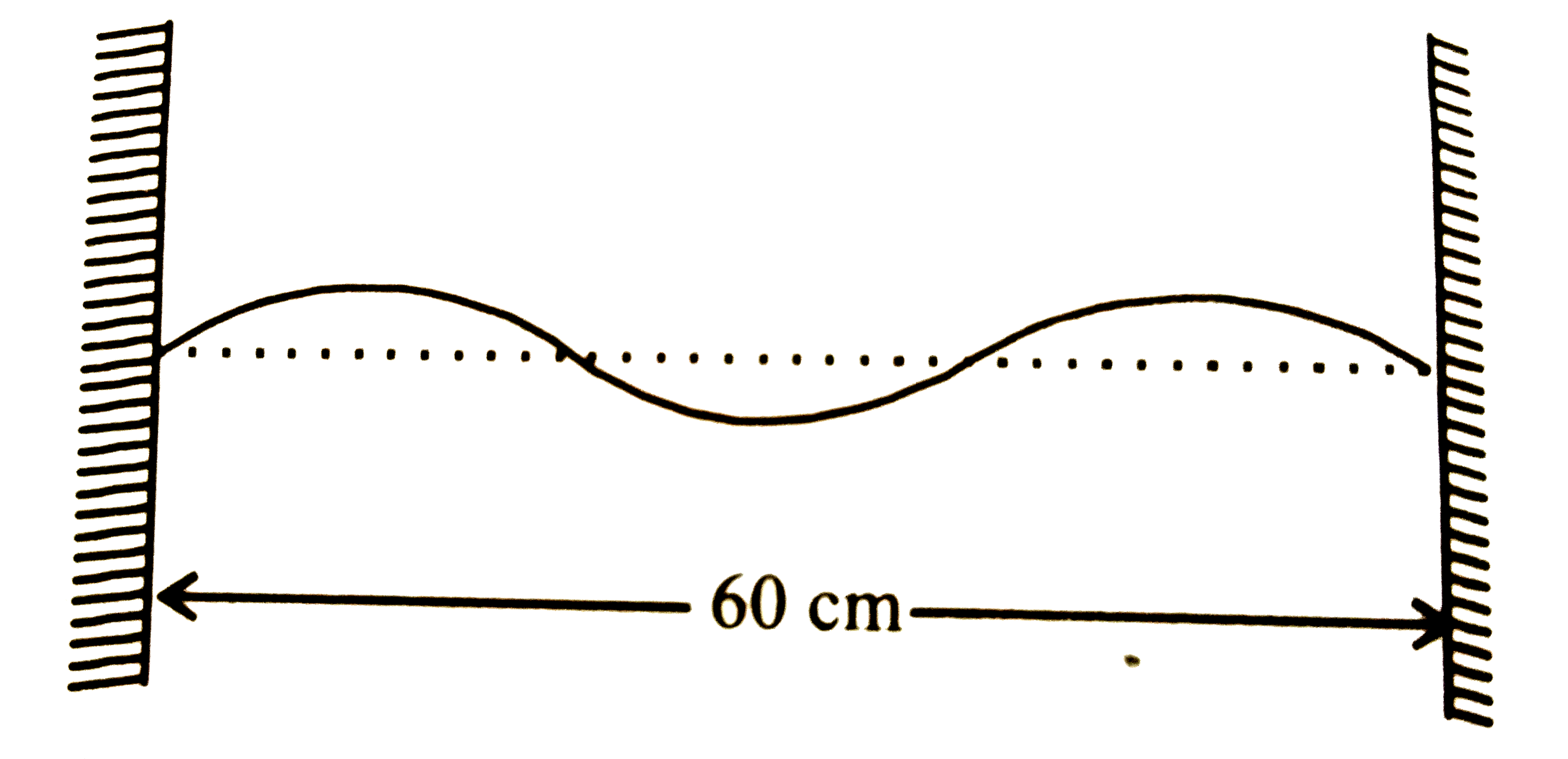
The standing wave pattern along a string of length 60 cm is shown in the above diagram. If the speed of the transverse waves on this string is 300 m/s, in which one of the following modes is the string vibrating?
View Solution
