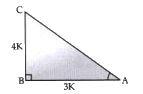
△ABC is a right triangle , right angle at B . Given the ratio of altitude and base tanA=43 . Find the value of (1+tan2A)
259
925
1625
2516
Step by step video & image solution for /_\ABC is a right triangle , right angle at B . Given the ratio of altitude and base tan A = 4/3 . Find the value of (1+tan^(2) A) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- INTRODUCTION TO TRIGONOMETRY AND TRIGONOMETRIC IDENTITIES BOOK - OSWAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRY AND TRIGONOMETRIC IDENTITIES EXERCISE - NCERT CORNER (Textbook Questions) (Exercise - 8.1)
18 Videos
- INTRODUCTION TO TRIGONOMETRY AND TRIGONOMETRIC IDENTITIES BOOK - OSWAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRY AND TRIGONOMETRIC IDENTITIES EXERCISE - NCERT CORNER (Textbook Questions) (Exercise - 8.2)
15 Videos
- INTRODUCTION TO TRIGONOMETRY AND TRIGONOMETRIC IDENTITIES BOOK - OSWAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRY AND TRIGONOMETRIC IDENTITIES EXERCISE - SELF ASSESSMENT - 2 (I. Objective Type Questions)(IV.Long Answer Type Questions - II)
3 Videos
- INTRODUCTION TO TRIGONOMETRY BOOK - OSWAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRY EXERCISE - Self - Assessment
15 Videos
- LINES (IN TWO - DIMENSIONS)BOOK - OSWAL PUBLICATIONCHAPTER - LINES (IN TWO - DIMENSIONS)EXERCISE - BOARD CORNER (LONG ANSWER TYPE QUESTION)
2 Videos
Similar Questions
Knowledge Check
In a triangle ABC, right angled at C, find the value of tan A + tan B in terms of the sides a,b,c.
Aa2bcBa+bCb2acDc2ab
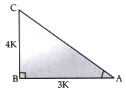
△ABC is a right triangle , right angle at B . Given the ratio of altitude and base tanA=43. Find the ratio of sin A
View Solution
ΔABC is a right triangle , right angle at B . Given the ratio of altitude and base tanA=43 .Find the value of sinA×tanA
View SolutionABC is right triangle , right angled at A, then tanB⋅tanC=_____
View SolutionIn a triangle ABC, right angled at B, then
View Solutionif in triangle ABC right angled at C then tanA+tanB
View SolutionABC is a right triangle, right angled at C and AB=√2BC. Then, find ∠ABC.
View SolutionIn a right triangle BC , right angled at B, the ratio of AB→AC is 1:√2 . Find the values of 2tanA1+tan2A and (ii) 2tanA1−tan2A
View Solution