If is isosceles with and is the incircle of the touching at , prove that bisects .
Step by step video & image solution for If A B C is isosceles with A B=A C and C(O ,\ r) is the incircle of the A B C touching B C at L , prove that L bisects B C . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -IV: Geometry (Circles) (Short Answer type questions)
22 Videos
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -IV: Geometry (Constructions) (VERY SHORT ANSWER TYPE QUESTIONS)
2 Videos
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -IV: Geometry (Circles) (Multiple Choice Questions)
13 Videos
- COORDINATE GEOMETRYBOOK - OSWAL PUBLICATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - SELF ASSESSMENT
20 Videos
- INTRODUCTION TO TRIGONOMETRY BOOK - OSWAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRY EXERCISE - Self - Assessment
15 Videos
Similar Questions
If ABC is isosceles with AB=AC and C(O, r) is the incircle of the ABC touching BC at L , prove that L bisects BC .
View SolutionIn Figure, ABC is an isosceles triangle in which AB=AC.CPparel≤lAB and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA and (ii) ABCP is a parallelogram.

View SolutionIf ABC ≅ACB, then ABC is isosceles with AB=AC (b) AB=BC AC=BC (d) None of these
View SolutionIf ABC is an isosceles triangle such that AB=AC and AD is an altitude from A on BC . Prove that (i) ∠B=∠C (ii) AD bisects BC (iii) AD bisects ∠A
View SolutionIn Figure, BD and CE are two altitudes of a ABC such that BD=CE. Prove that ABC is isosceles.
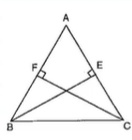
View SolutionIn ABC , AL and CM are the perpendiculars from the vertices A and C to BC and AB respectively. If AL and CM intersect at O , prove that: (i) OMAOLC (ii) OAOC=OMOL
View SolutionD is the mid-point of side BC of ABC and E is the mid-point of BD. If O is the mid-point of AE , prove that ar(BOE)=18ar(ABC)
View SolutionIn an isosceles triangle ABC, with AB=AC, the bisectors of B and C intersect each other at O. Join A to O. Show that :
(i) OB=OC
(ii) AO bisects A
View SolutionTriangles ABC and +DBC are on the same base BC with A, D on opposite side of line BC, such that ar(△ABC)=ar(△DBC). Show that BC bisects AD.
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣CD . Prove that: ar(AOD)=ar(BOC).

View Solution
