Draw two concentric circles of radii 3 cm and 5 cm . Construct a tangent to smaller circle from a point on the larger circle . Also measure its length.
Step-by-Step Solution:
Step 1: Draw the Concentric Circles
1. Use a compass to draw a circle with a radius of 5 cm. This will be the larger circle.
2. Without changing the compass width, place the compass point at the center of the larger circle and draw a second circle with a radius of 3 cm. This will be the smaller circle.
Step 2: Mark a Point on the Larger Circle
1. Choose any point on the circumference of the larger circle. Label this point as P.
Step 3: Draw a Radius to the Smaller Circle
1. Draw a line from the center of the circles (let's call it O) to the point P. This line represents the radius of the larger circle.
Step 4: Draw a Tangent to the Smaller Circle
1. From point P, draw a line that touches the smaller circle at exactly one point. This line is the tangent to the smaller circle. Label the point of tangency as T.
Step 5: Measure the Length of the Tangent
1. To find the length of the tangent PT, we can use the Pythagorean theorem.
2. The radius of the smaller circle OT is 3 cm, and the radius of the larger circle OP is 5 cm.
3. The line segment OP is the hypotenuse, and OT is one leg of the right triangle OTP. The length of the tangent PT is the other leg.
Step 6: Apply the Pythagorean Theorem
1. According to the Pythagorean theorem:
OP2=OT2+PT2
Substituting the values:
52=32+PT2
25=9+PT2
PT2=25−9
PT2=16
PT=√16=4 cm
Final Answer:
The length of the tangent PT from point P on the larger circle to the smaller circle is 4 cm.
---
1. Use a compass to draw a circle with a radius of 5 cm. This will be the larger circle.
2. Without changing the compass width, place the compass point at the center of the larger circle and draw a second circle with a radius of 3 cm. This will be the smaller circle.
1. Choose any point on the circumference of the larger circle. Label this point as P.
1. Draw a line from the center of the circles (let's call it O) to the point P. This line represents the radius of the larger circle.
1. From point P, draw a line that touches the smaller circle at exactly one point. This line is the tangent to the smaller circle. Label the point of tangency as T.
1. To find the length of the tangent PT, we can use the Pythagorean theorem.
2. The radius of the smaller circle OT is 3 cm, and the radius of the larger circle OP is 5 cm.
3. The line segment OP is the hypotenuse, and OT is one leg of the right triangle OTP. The length of the tangent PT is the other leg.
1. According to the Pythagorean theorem:
OP2=OT2+PT2
Substituting the values:
52=32+PT2
25=9+PT2
PT2=25−9
PT2=16
PT=√16=4 cm
The length of the tangent PT from point P on the larger circle to the smaller circle is 4 cm.
Topper's Solved these Questions
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - UNIT -V: Trigonometry (Introduction to Trigonometry ) (MULTIPLE CHOICE QUESTIONS)
4 Videos
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - UNIT -V: Trigonometry (Introduction to Trigonometry ) (VERY SHORT ANSWER TYPE QUESTIONS )
15 Videos
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -IV: Geometry (Constructions) (VERY SHORT ANSWER TYPE QUESTIONS)
2 Videos
- COORDINATE GEOMETRYBOOK - OSWAL PUBLICATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - SELF ASSESSMENT
20 Videos
- INTRODUCTION TO TRIGONOMETRY BOOK - OSWAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRY EXERCISE - Self - Assessment
15 Videos
Similar Questions
Draw two concentric circles of radii 3 cm and 5 cm. Construct a tangent to the smaller circle from a point on the larger circle. Also, measure its length.
View SolutionDraw two circles of radii 6 cm and 4 cm. From a point on the outer circle, draw a tangent to the inner circle and measure its length.
View Solution
Knowledge Check
The radius of the two concentric circles is 5 cm and 13 cm. The tangent to the smaller circle is the chord to the greater circle. What is the length (in cm) of that chord?
A12B20C22D24The radius of the two concentric circles is 5 cm and 13 cm. The tangent to the smaller circle is the chord to the greater circle. What is the length (in cm) of that chord?
A12B20C22D24Two concentric circles are of radii 13 cm and 5 cm. The length of the chord of the larger circle which touches the smaller circle is:
दो संकेंद्री वृत्तों की त्रिज्या 13 सेमी तथा 5 सेमी है। बड़े वृत्त की जीवा की लंबाई ज्ञात कीजिए, जो छोटे वृत्त को स्पर्श करती है।A6 cmB7 cmC10 cmD8 cm
Draw two concentric circles of radii 3 cm and 5 cm . Taking a point on outer circle construct the pair of tangents to the other. Measure the length of a tangent and verify it by actual calculation .
View SolutionDraw a circle of radius 2.6 cm. Draw a tangent to the circle from any point on the circle.
View SolutionDraw two concentric circles of radii 3 cm and 5 cm. Taking a point on outer circle, construct the pair of tangents to the other. Measure the length of a tangent and verify is by actual calculation.
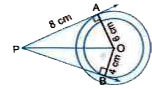
View SolutionIn Fig , are two concentric circles of radii 6 cm and 4 cm with centre O . If AP is a tangent to the larger circle and BP to the smaller circle and length of AP is 8 cm, find the length of BP.
View SolutionDraw two concentric circles of radius 3.5 cm and 5 cm. Label point P in exterior of bigger circle and smaller circle.
View Solution