In triangle ABC, right angled at B, AC = 20 m, ∠C=45∘, find the value of AB.
To solve the problem, we will use the properties of a right-angled triangle.
1. Identify the Triangle and Given Values:
- We have triangle ABC with a right angle at B.
- The length of hypotenuse AC is given as 20 m.
- Angle C is given as 45°.
2. Use the Sine Function:
- In a right-angled triangle, the sine of an angle is defined as the ratio of the length of the opposite side (perpendicular) to the length of the hypotenuse.
- Here, we need to find the length of side AB (which is opposite to angle C).
3. Write the Sine Formula:
- For angle C (45°):
sinC=ABAC
- Substituting the known values:
sin45°=AB20
4. Substitute the Value of Sine 45°:
- We know that:
sin45°=1√2
- Therefore, we can write:
1√2=AB20
5. Cross-Multiply to Solve for AB:
- Cross-multiplying gives:
AB=20×1√2
- This simplifies to:
AB=20√2
6. Rationalize the Denominator:
- To simplify 20√2, we multiply the numerator and denominator by √2:
AB=20√22=10√2
7. Final Answer:
- Thus, the length of AB is:
AB=10√2 meters
- We have triangle ABC with a right angle at B.
- The length of hypotenuse AC is given as 20 m.
- Angle C is given as 45°.
- In a right-angled triangle, the sine of an angle is defined as the ratio of the length of the opposite side (perpendicular) to the length of the hypotenuse.
- Here, we need to find the length of side AB (which is opposite to angle C).
- For angle C (45°):
sinC=ABAC
- Substituting the known values:
sin45°=AB20
- We know that:
sin45°=1√2
- Therefore, we can write:
1√2=AB20
- Cross-multiplying gives:
AB=20×1√2
- This simplifies to:
AB=20√2
- To simplify 20√2, we multiply the numerator and denominator by √2:
AB=20√22=10√2
- Thus, the length of AB is:
AB=10√2 meters
Topper's Solved these Questions
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - UNIT -V: Trigonometry (Heights and Distances) (Short Answer Type Questions )
8 Videos
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - UNIT -V: Trigonometry (Heights and Distances) (Long Answer Type Questions)
10 Videos
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - UNIT -V: Trigonometry (Heights and Distances) (MULTIPLE CHOICE QUESTIONS)
3 Videos
- COORDINATE GEOMETRYBOOK - OSWAL PUBLICATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - SELF ASSESSMENT
20 Videos
- INTRODUCTION TO TRIGONOMETRY BOOK - OSWAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRY EXERCISE - Self - Assessment
15 Videos
Similar Questions
Knowledge Check
ΔABC is right angled at B.If m∠A=45∘,then find the value of (tanC+√32).
A4/√3B(2+√3)/2C(√2+2)/2√2D(2+√3)/3In a ΔABC right - angled at B, AB : AC = 1 : 2. Then the value of cotA+tanCsinB+cosB is:
A2√3B√3+12C2√2−√22D√3−1
In ΔABC,right -angled at B,AB=5cmandBC=12cm. find the values of sinA,secA,sinCandsecC.
View SolutionIn the given figure,ABC in a right-angled triangle,right-angled atB.IfBC=5cmandAC-AB=1cm,f∈dthevalueofcosecAandcos A
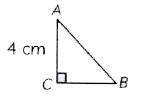
View SolutionIn Figure ABC is an isosceles triangle right angled at C with AC = 4 cm . Find the length of AB .
View SolutionIf in a triangle ABC right angled at B, AB = 6 units and BC = 8 units, then find the value of sin A. cos C + cos A. sin C.
View SolutionIn the given figure, △ABC is an isosceles triangle right angled at C with AC = 4 cm. Find the length of AB.
View SolutionIn a right-angled triangle ABC, right angled at B, AB = x2, BC = x+2 and AC = x+3. Find value of x.
View Solution
