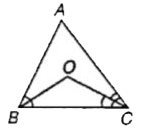
In the given figure , AB = AC , ∠BAC=40∘ , BE and CD are angle bisectors of ∠Band∠C respectively . If ∠DOE=x , the value of x is :
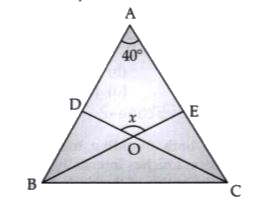
140∘
70∘
110∘
40∘
The correct Answer is:C
Step by step video & image solution for In the given figure , AB = AC , angle BAC = 40^(@) , BE and CD are angle bisectors of angleB and angleC respectively . If angleDOE = x , the value of x is : by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NTSE 2019 -20BOOK - OSWAL PUBLICATIONCHAPTER - NTSE 2019 -20EXERCISE - Triangles Stage -2
1 Videos
- NTSE 2019 -20BOOK - OSWAL PUBLICATIONCHAPTER - NTSE 2019 -20EXERCISE - Circles Stage -1
2 Videos
- NTSE 2019 -20BOOK - OSWAL PUBLICATIONCHAPTER - NTSE 2019 -20EXERCISE - Coordinate Geometry Stage -2
1 Videos
- NEW TYPOLOGIES INTRODUCED BY CBSE FOR BOARD 2021-22 EXAM BOOK - OSWAL PUBLICATIONCHAPTER - NEW TYPOLOGIES INTRODUCED BY CBSE FOR BOARD 2021-22 EXAM EXERCISE - UNIT-VII STATISTICS AND PROBABILITY (STATISTICS) (SELF ASSESSMENT)
2 Videos
- OLYMPIAD 2019-20BOOK - OSWAL PUBLICATIONCHAPTER - OLYMPIAD 2019-20EXERCISE - 15. Probability
1 Videos
Similar Questions
Knowledge Check
In the given diagram of ΔABC,∠B=80∘,∠C=30∘ BF and CF are the angle bisectors of ∠CBDand∠BCE respectively. Find the value of ∠BFC :
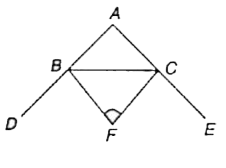 A110∘B50∘C125∘D55∘
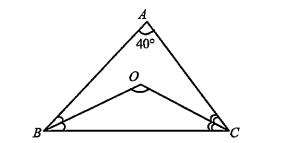
A110∘B50∘C125∘D55∘In given triangle ABC ,OB and OC are bisectors of ∠Ba nd ∠C respectively then ∠BOC is equal to
 A70∘B110∘C140∘D80∘
A70∘B110∘C140∘D80∘In a triangle ABC , OB and OC are the bisector of angle ∠B and ∠C respectively . ∠BAC=60∘ . The angle ∠BOC will be :
A150∘B120∘C100∘D90∘
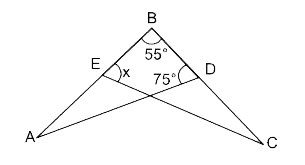
In the given figure , if AB=BC and ∠A=∠C then find the value of x
View SolutionIn the given figure, AB∣∣CD. Find the value of x.
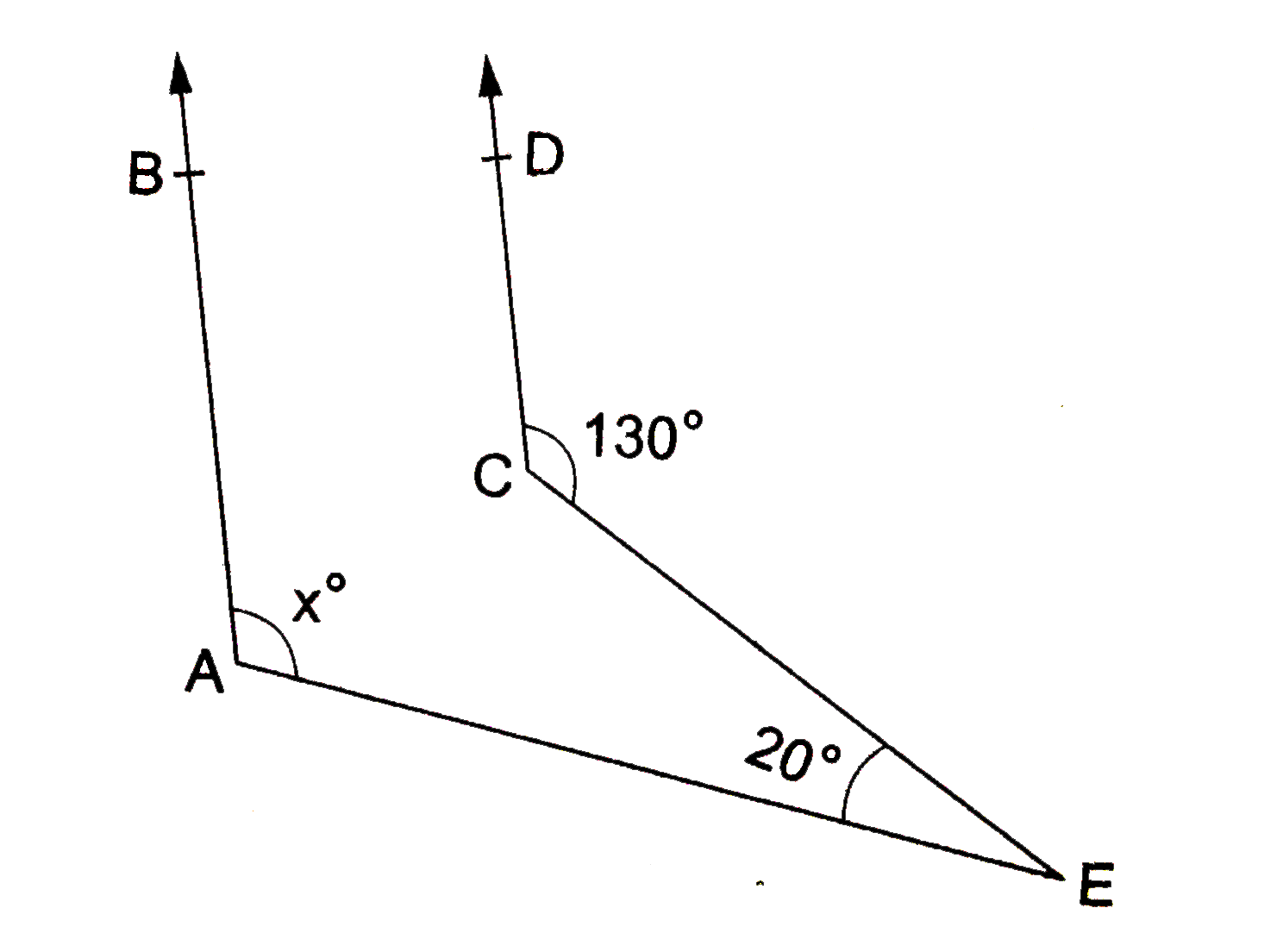
View SolutionIn the given figure, AB∣∣CD. Find the value of x.

View SolutionIn the following figure ∠B=70∘ and ∠C=30∘.BOandCO are the angle bisectors of ∠ABCand∠ACB. Find the value of ∠BOC:
View SolutionIn the given figure, ∠A=80∘,∠B=60∘,∠C=2x∘and∠BDC=y∘. BD and CD bisect angles B and C respectively.
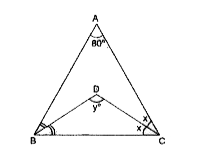
The values of x and y respectively are :
View Solution