ΔABC is isosceles with AC = BC . If AB2=2AC2 then find the measure of ∠C
The correct Answer is:90∘
To solve the problem, we need to find the measure of angle C in triangle ABC, given that AC = BC and AB² = 2AC².
1. Identify the Given Information:
- Triangle ABC is isosceles with AC = BC.
- We have the equation: AB² = 2AC².
2. Substitute AC for BC:
- Since AC = BC, we can replace BC in the equation. Thus, we rewrite AB²:
AB²=2AC²
3. Use the Isosceles Triangle Property:
- In triangle ABC, since AC = BC, we can denote AC as 'x'. Therefore:
AB²=2x²
4. Apply the Cosine Rule:
- In triangle ABC, we can apply the cosine rule:
AB²=AC²+BC²−2⋅AC⋅BC⋅cos(C)
Substituting AC and BC with 'x':
AB²=x²+x²−2x²⋅cos(C)
Simplifying this gives:
AB²=2x²−2x²⋅cos(C)
5. Set the Two Expressions for AB² Equal:
- From the earlier step, we have:
2x²=2x²−2x²⋅cos(C)
Rearranging this gives:
0=−2x²⋅cos(C)
6. Solve for cos(C):
- Since −2x² cannot be zero (x is a length), we can conclude:
cos(C)=0
7. Determine the Angle C:
- The angle C for which cos(C) = 0 is:
C=90∘
Conclusion:
The measure of angle C is 90∘.
- Triangle ABC is isosceles with AC = BC.
- We have the equation: AB² = 2AC².
- Since AC = BC, we can replace BC in the equation. Thus, we rewrite AB²:
AB²=2AC²
- In triangle ABC, since AC = BC, we can denote AC as 'x'. Therefore:
AB²=2x²
- In triangle ABC, we can apply the cosine rule:
AB²=AC²+BC²−2⋅AC⋅BC⋅cos(C)
Substituting AC and BC with 'x':
AB²=x²+x²−2x²⋅cos(C)
Simplifying this gives:
AB²=2x²−2x²⋅cos(C)
- From the earlier step, we have:
2x²=2x²−2x²⋅cos(C)
Rearranging this gives:
0=−2x²⋅cos(C)
- Since −2x² cannot be zero (x is a length), we can conclude:
cos(C)=0
- The angle C for which cos(C) = 0 is:
C=90∘
The measure of angle C is 90∘.
Topper's Solved these Questions
- C.B.S.E 2020 CLASS -X (DELHI)BOOK - OSWAL PUBLICATIONCHAPTER - C.B.S.E 2020 CLASS -X (DELHI)EXERCISE - DELHI SET -II ( SECTION- B )
2 Videos
- C.B.S.E 2020 CLASS -X (DELHI)BOOK - OSWAL PUBLICATIONCHAPTER - C.B.S.E 2020 CLASS -X (DELHI)EXERCISE - DELHI SET -II ( SECTION- C )
3 Videos
- C.B.S.E 2020 CLASS -X (DELHI)BOOK - OSWAL PUBLICATIONCHAPTER - C.B.S.E 2020 CLASS -X (DELHI)EXERCISE - DELHI SET -I ( SECTION-C )
20 Videos
- ARITHMETIC PROGRESSIONS BOOK - OSWAL PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONS EXERCISE - CASE - BASED MCQs
15 Videos
- C.B.S.E 2020 CLASS -X (OUTSIDE DELHI)BOOK - OSWAL PUBLICATIONCHAPTER - C.B.S.E 2020 CLASS -X (OUTSIDE DELHI)EXERCISE - OUTSIDE DELHI SET -III ( SECTION- D )
2 Videos
Similar Questions
Knowledge Check
In an isosceles ΔABC, if AC=BC and AB2=2AC2 then ∠C=?
A30∘B45∘C60∘D90∘ΔABC is an isosceles triangles with AB = AC = 10 cm,AD =8 cm M is the median on BC from A. The length of BC is
A8 cmB12 cmC10 cmD6 cm
ABC is an isosceles triangle with AC = BC. If AB2=2AC2, prove that ABC is a right triangle.
View SolutionABC is an isosceles triangle with AC = BC. If AB2−2AC2=0, prove that ABC is right triangle.
View SolutionIn ΔABC, AP is a median. If AP=7,AB2+AC2=260, then find BC.
View SolutionIn ΔABC,∠BAC=120∘ and AB = AC, then find measure of ∠ABC.
View SolutionIn a triangle ABC, if ∠A=70∘andAB=AC, then find the measures of ∠Band∠C.
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
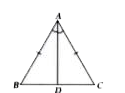
∠B=∠C
View Solution