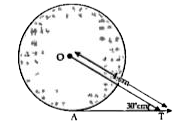
AT is a tangent to circle with centres such that OT = 4 cm and ∠OTA=30∘. Find the length of AT.

The correct Answer is:2√3cm
Step by step video, text & image solution for AT is a tangent to circle with centres such that OT = 4 cm and angle OTA = 30^(@). Find the length of AT. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 8EXERCISE - PART-A (SECTION-II)20videos
SAMPLE PAPER 8
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 8EXERCISE - PART-B (SECTION-III)9videos
SAMPLE PAPER 8
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 8EXERCISE - SECTION-C10videos
SAMPLE PAPER 8
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - PART - B (SECTION - V)8videos
SAMPLE PAPER 7
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 9EXERCISE - SECTION C10videos
SAMPLE PAPER 9
Similar Questions
Knowledge Check
- Question 1 - Select One
In figure, AT is a tangent to the circle with centre 0 such that OT = 4 cm and ∠OTA=30∘. Then, AT is equal to
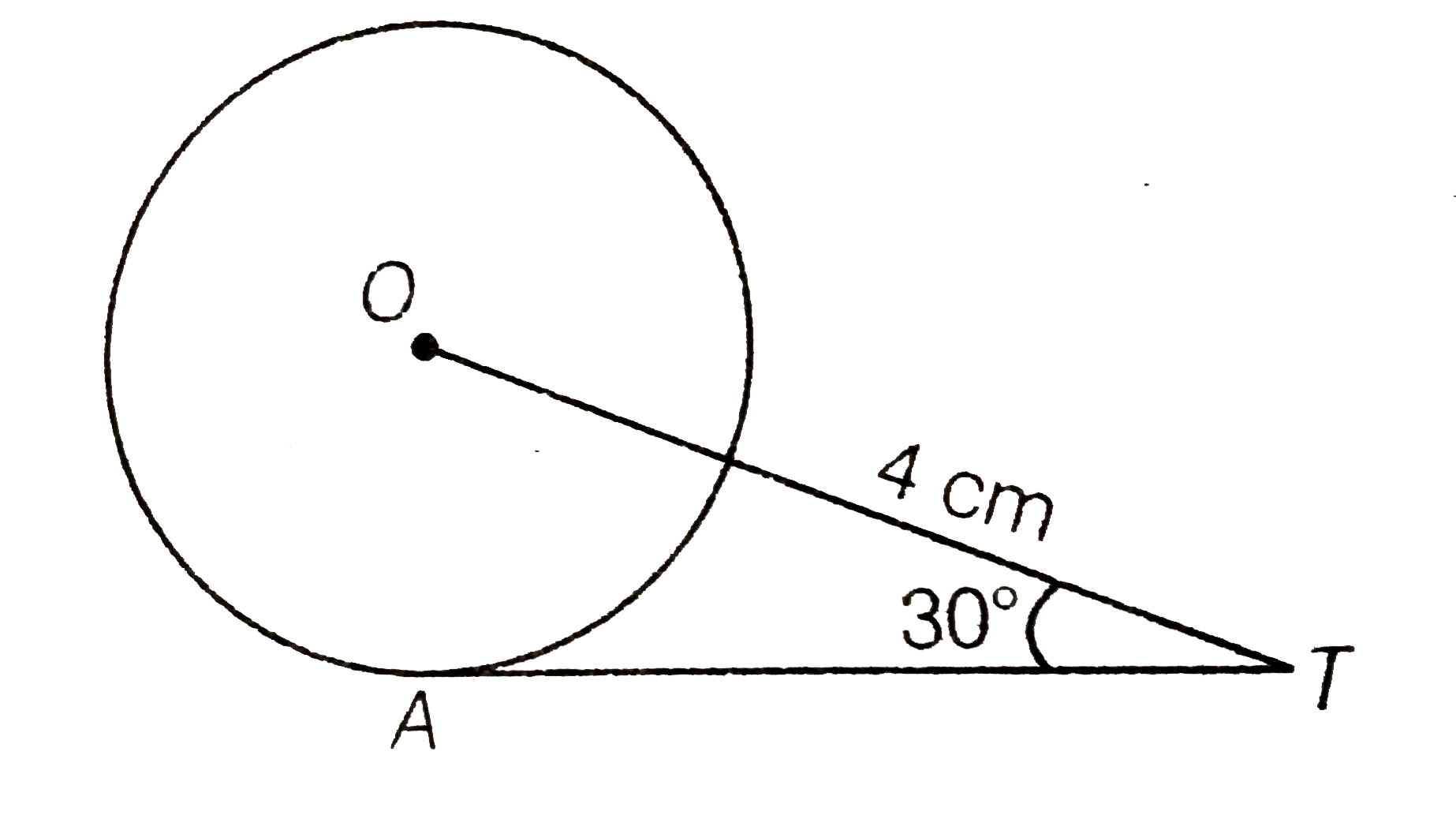 A4 cmB2 cmC2√3cmD4√3cm
A4 cmB2 cmC2√3cmD4√3cm - Question 2 - Select One
AB is a tangent to a circle with centre O. If the radius at the circle is 7 cm and the length of AB is 24 cm, then what is the length (in cm) of OA?
A25B26C28D31
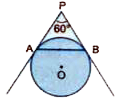
In Fig AP and BP are tangents to a circle with centre O, such that AP = 5 cm , and ∠APB=60∘ . Find the length of chord AB.
 View Solution
View SolutionIn Fig PT is a tangent to the circle (O,r) such that OT=6√3 units and ∠OTP=30∘ Find the length of PT.
 View Solution
View SolutionIn the given figure, PT is a tangent to the circle with centre O. If OT=6cm and OP=10cm, thcn find the length of tangent PT.
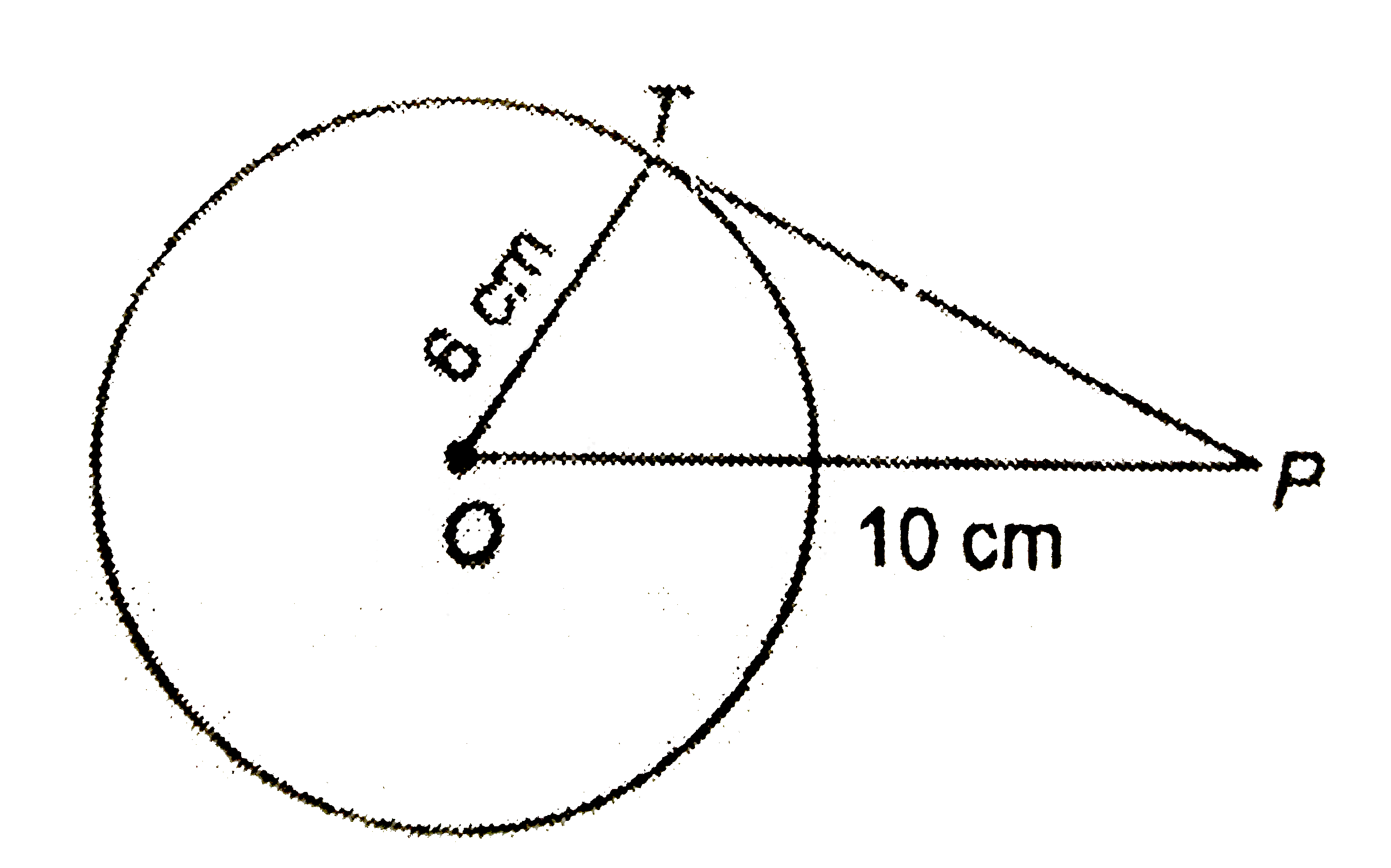 View Solution
View SolutionIn fig. PQ is a tangent to length 6cm to the circle with centre O and ∠OQP=60∘ . Find OQ
 View Solution
View SolutionIn the adjoining figure ,PT is tangent to a circle with centre O . if OP= 25 cm and radius of circle is 7cm , then find the length of the tangent PT .
View SolutionIf PT is a tangent at T to a circle whose centre is O and OP=17cm , OT=8cm , Find the length of the tangent segment PT .
View Solution