In the figure,

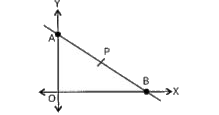
If P is the point (- $cos θ, sin θ$ ), then find the length of OP, where O is the origin.

Video Solution

Answer

Step by step video & image solution for In the figure, If P is the point (-costheta,sintheta), then find the length of OP, where O is the origin. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023

Class 10 MATHS QUESTION BANK

Topper's Solved these Questions

SAMPLE PAPER (SELF ASSESSMENT) 12BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER (SELF ASSESSMENT) 12EXERCISE - PART-A (Section-II)
20 Videos
SAMPLE PAPER (SELF ASSESSMENT) 12BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER (SELF ASSESSMENT) 12EXERCISE - PART-B (Section-III)
8 Videos
SAMPLE PAPER 5 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5 EXERCISE - Part B (Section - V)
4 Videos
SAMPLE PAPER - 11BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER - 11EXERCISE - SECTION-C
10 Videos

Knowledge Check

If $y = x + c$ touches the ellipse $3 x^{2} + 4 y^{2} = 12$ at the point P, then the value of the length OP (where O is the origin) is equal to
A $\sqrt{3}$ units
B $\sqrt{7}$ units
C $\frac{5}{\sqrt{7}}$ units
D $\sqrt{\frac{7}{5}}$ units

EDUCART PUBLICATION-SAMPLE PAPER (SELF ASSESSMENT) 12-PART-B (Section-V)

Home
Ask Doubt
Profile

In the figure, If P is the point (-cosθ,sinθ), then find the length of OP, where O is the origin.

Topper's Solved these Questions

Similar Questions

Knowledge Check

If y=x+c touches the ellipse 3x2+4y2=12 at the point P, then the value of the length OP (where O is the origin) is equal to

EDUCART PUBLICATION-SAMPLE PAPER (SELF ASSESSMENT) 12-PART-B (Section-V)

In the figure,

If P is the point (- $cos θ, sin θ$ ), then find the length of OP, where O is the origin.

If $y = x + c$ touches the ellipse $3 x^{2} + 4 y^{2} = 12$ at the point P, then the value of the length OP (where O is the origin) is equal to