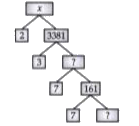
Make a factor tree for the composite number 324.
To create a factor tree for the composite number 324, we will break it down into its prime factors step by step.
1. Start with the number 324:
- We begin with the composite number 324.
2. Find two factors of 324:
- We can divide 324 by 2 (since it's even).
- \( 324 \div 2 = 162 \)
- So, we have: \( 324 = 2 \times 162 \)
3. Factor 162:
- Next, we take 162 and find its factors. Again, 162 is even, so we can divide by 2.
- \( 162 \div 2 = 81 \)
- Now we have: \( 162 = 2 \times 81 \)
- Thus, \( 324 = 2 \times 2 \times 81 \)
4. Factor 81:
- Now we need to factor 81. The number 81 is not even, so we check for divisibility by 3.
- \( 81 \div 3 = 27 \)
- So, we have: \( 81 = 3 \times 27 \)
- Thus, \( 324 = 2 \times 2 \times 3 \times 27 \)
5. Factor 27:
- Next, we factor 27. Again, we can divide by 3.
- \( 27 \div 3 = 9 \)
- So, we have: \( 27 = 3 \times 9 \)
- Thus, \( 324 = 2 \times 2 \times 3 \times 3 \times 9 \)
6. Factor 9:
- Finally, we factor 9. We can divide it by 3.
- \( 9 \div 3 = 3 \)
- So, we have: \( 9 = 3 \times 3 \)
- Thus, \( 324 = 2 \times 2 \times 3 \times 3 \times 3 \times 3 \)
7. Write the prime factorization:
- Now we can combine all the prime factors:
- \( 324 = 2^2 \times 3^4 \)
Final Factor Tree Representation:
32421622813273933
- We begin with the composite number 324.
- We can divide 324 by 2 (since it's even).
- \( 324 \div 2 = 162 \)
- So, we have: \( 324 = 2 \times 162 \)
- Next, we take 162 and find its factors. Again, 162 is even, so we can divide by 2.
- \( 162 \div 2 = 81 \)
- Now we have: \( 162 = 2 \times 81 \)
- Thus, \( 324 = 2 \times 2 \times 81 \)
- Now we need to factor 81. The number 81 is not even, so we check for divisibility by 3.
- \( 81 \div 3 = 27 \)
- So, we have: \( 81 = 3 \times 27 \)
- Thus, \( 324 = 2 \times 2 \times 3 \times 27 \)
- Next, we factor 27. Again, we can divide by 3.
- \( 27 \div 3 = 9 \)
- So, we have: \( 27 = 3 \times 9 \)
- Thus, \( 324 = 2 \times 2 \times 3 \times 3 \times 9 \)
- Finally, we factor 9. We can divide it by 3.
- \( 9 \div 3 = 3 \)
- So, we have: \( 9 = 3 \times 3 \)
- Thus, \( 324 = 2 \times 2 \times 3 \times 3 \times 3 \times 3 \)
- Now we can combine all the prime factors:
- \( 324 = 2^2 \times 3^4 \)
32421622813273933
Topper's Solved these Questions
- SAMPLE PAPER 13BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 13EXERCISE - PART A (SECTION-II)
8 Videos
- SAMPLE PAPER 13BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 13EXERCISE - PART B (SECTION-III)
8 Videos
- SAMPLE PAPER 11 (SELF - ASSESSMENT)BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 11 (SELF - ASSESSMENT)EXERCISE - SECTION -C
10 Videos
- SAMPLE PAPER 2 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 2 EXERCISE - SECTION - D
9 Videos
Similar Questions
Knowledge Check
What is a composite number ?
AA number having only 2 factors i.e. 1 and itselfBA number having at least 3 factors is called is called a composite number.CA number which is divisible by 2Dnone of theseIn a set of prime and composite numbers, the composite numbers are twice the number of prime numbers and the average of all the number of the set is 9. If the number of prime numbers and composite numbers are exchanged then the average of the set of numbers is increased by 2. If during the exchange of the numbers the average of the prime numbers and composite numbers individually remained constant, then the ratio of the average of composite numbers to the average of prime numbers (initially) was :
A7/13B13/7C9/11Dnone of these
What is a composite number?
View SolutionDraw factor tree for the following:
102
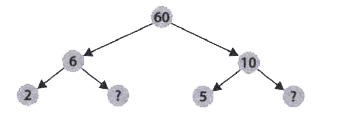
View SolutionHere are two different factor trees for 60. Write the missing numbers.
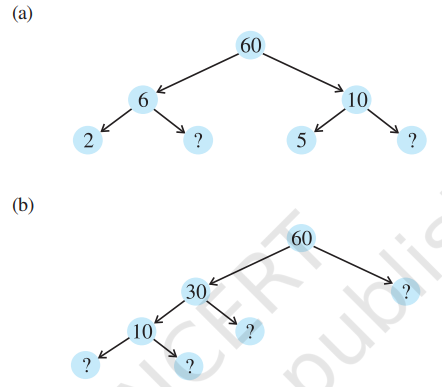
View SolutionHere are two different factor trees for 60. Write the missing numbers.
View SolutionWhich factors are not included in the prime factorization of a composite number?
View SolutionWhich factors are not included in the prime factorisation of a composite number?
View Solution