A stop sign is an example of a Polygon, in the image, you can see examples of diagonals in geometry in the stop sign. Hence, there a various number of diagonals possible in a Polygon.

The number of diagonals (d) that can be drawn in polygons with a given number of sides (n) is being investigated.


On the basis of the above information, answer any four of the following questions:
For a polygon, d and n are related as d=An2 + Bn . The relations for a triangle and a quadrilateral are
3A + B = 0, 8A + 2B.= 1
9A + 3B = 0, 5A + B = 1
3A + B = 0, 12A + 2 B = 3
3A + B = 0, 8A + 5 B=3
Step by step video & image solution for A stop sign is an example of a Polygon, in the image, you can see examples of diagonals in geometry in the stop sign. Hence, there a various number of diagonals possible in a Polygon. The number of diagonals (d) that can be drawn in polygons with a given number of sides (n) is being investigated. On the basis of the above information, answer any four of the following questions: For a polygon, d and n are related as d = An^(2) + Bn . The relations for a triangle and a quadrilateral are by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SAMPLE PAPER 12 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 12 EXERCISE - PART - B (SECTION -III)
9 Videos
- SAMPLE PAPER 12 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 12 EXERCISE - PART - B (SECTION -IV)
9 Videos
- SAMPLE PAPER 12 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 12 EXERCISE - PART - B (SECTION -V)
4 Videos
- SAMPLE PAPER - 6 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER - 6 EXERCISE - PART - B (SECTION - IV)
13 Videos
- SAMPLE PAPER 5 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5 EXERCISE - Part B (Section - V)
4 Videos
Similar Questions
A stop sign is an example of a Polygon, in the image, you can see examples of diagonals in geometry in the stop sign. Hence, there a various number of diagonals possible in a Polygon.

The number of diagonals (d) that can be drawn in polygons with a given number of sides (n) is being investigated.
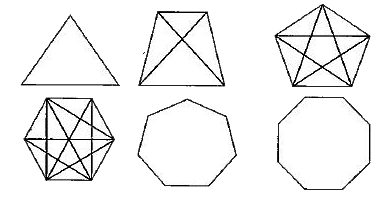

On the basis of the above information, answer any four of the following questions:
By considering the pattern, the value of q' is
View SolutionA stop sign is an example of a Polygon. In the image , you can see examples of diagonals in geometry n the stop sign, there a various number of diagonals possible in a Polygon.

the number of diagonals (d) that can be drawn in polygons with a given number of sides (n) is being investigated.
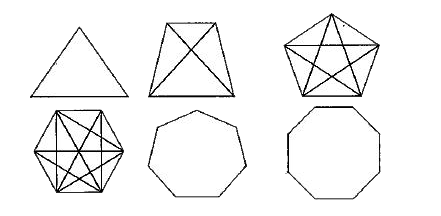

By considering the pattern, the value of 'p' is
View Solution
Knowledge Check
The number of diagonals in a polygon of m sides is
A12!m(m−5)B12!m(m−1)C12!m(m−3)D12!m(m−2)The number of diagonals of a polygon of n sides is
An(n−1)2Bn(n−3)2C(n−1)(n−2)2Dnone of theseThe number of diagonals of a polygon of 15 sides is
A105B90C75D60
The number of diagonals in a polygon is 20. The number of sides of the polygon is
View SolutionWrite the number of diagonals of an n-sided polygon.
View SolutionFind the number of diagonals of a 16-sided polygon.
View SolutionFind the number of diagonals in an n-sided polygon.
View SolutionThe number of diagonals of a polygon of 15 sides is:
View Solution
