In ΔABC,∠B=90∘ and d is the mid - point of BC. Prove that AC2=AD2+3CD2
To prove that AC2=AD2+3CD2 in triangle ABC where ∠B=90∘ and D is the midpoint of BC, we can follow these steps:
1. Identify the Given Information:
- Triangle ABC with ∠B=90∘.
- D is the midpoint of BC.
2. Apply the Pythagorean Theorem:
- In triangle ABD:
AB2+AD2=AC2(1)
- In triangle BCD:
BD2+CD2=BC2(2)
3. Express BC in terms of BD and CD:
- Since D is the midpoint of BC, we have:
BD=CD
- Let BD=CD=x. Then, BC=BD+CD=x+x=2x.
4. Substitute BC in Equation (2):
- From Equation (2):
x2+x2=(2x)2
- This simplifies to:
2x2=4x2
- Thus, we have BC2=4x2.
5. Substituting BC2 back into the Pythagorean Theorem:
- From Equation (1):
AB2+AD2=AC2
- We need to express AB2 in terms of AD and CD.
6. Express AB2:
- From triangle BCD:
AB2=AC2−AD2
- Substitute BC2=4x2 into the equation:
AC2=AD2+2x2
7. Final Step:
- Now, we can express AC2:
AC2=AD2+3CD2
- Since CD=x, we have:
AC2=AD2+3x2
- Therefore, we have proved that:
AC2=AD2+3CD2
- Triangle ABC with ∠B=90∘.
- D is the midpoint of BC.
- In triangle ABD:
AB2+AD2=AC2(1)
- In triangle BCD:
BD2+CD2=BC2(2)
- Since D is the midpoint of BC, we have:
BD=CD
- Let BD=CD=x. Then, BC=BD+CD=x+x=2x.
- From Equation (2):
x2+x2=(2x)2
- This simplifies to:
2x2=4x2
- Thus, we have BC2=4x2.
- From Equation (1):
AB2+AD2=AC2
- We need to express AB2 in terms of AD and CD.
- From triangle BCD:
AB2=AC2−AD2
- Substitute BC2=4x2 into the equation:
AC2=AD2+2x2
- Now, we can express AC2:
AC2=AD2+3CD2
- Since CD=x, we have:
AC2=AD2+3x2
- Therefore, we have proved that:
AC2=AD2+3CD2
Topper's Solved these Questions
- SAMPLE PAPER 12 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 12 EXERCISE - PART - B (SECTION -V)
4 Videos
- SAMPLE PAPER 12 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 12 EXERCISE - PART - B (SECTION -III)
9 Videos
- SAMPLE PAPER - 6 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER - 6 EXERCISE - PART - B (SECTION - IV)
13 Videos
- SAMPLE PAPER 5 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5 EXERCISE - Part B (Section - V)
4 Videos
Similar Questions
In a triangle ABC,B=90∘ and D is the mid-point of BC then prove that AC2=AD2+3CD2
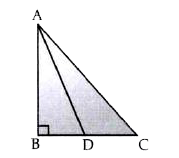
View SolutionIn the given figure ABC is a right angled triangle with ∠B=90∘ . D is the mid -point of BC . Show that AC2=AD2+3CD2 .
View SolutionIn ΔABC,∠A=90∘,AB=AC,D is any point on BC. Provew that BD2+CD2=2AD2.
View SolutionIn right-angled triangle ABC in which ∠C=90∘ , if D is the mid-point of BC , prove that AB2=4 AD2−3 AC2 .
View SolutionIn Fig. 3, ABC is a right triangle, right angled at C and D is the mid-point of BC. Prove that AB2=4AD2−3AC2.
View SolutionIn a right ABC right-angled at C , if D is the mid-point of BC , prove that BC2=4 (AD2−AC2) .
View SolutionIn a ΔABC,∠B is an acute-angle and AD⊥BC
Prove that :
(i) AC2=AB2+BC2−2BC×BD
(ii) AB2+CD2=AC2+BD2
View SolutionIn an isoscles ΔABC,AB=ACandD is a point on BC. Prove that AB2−AD2=BD⋅CD.
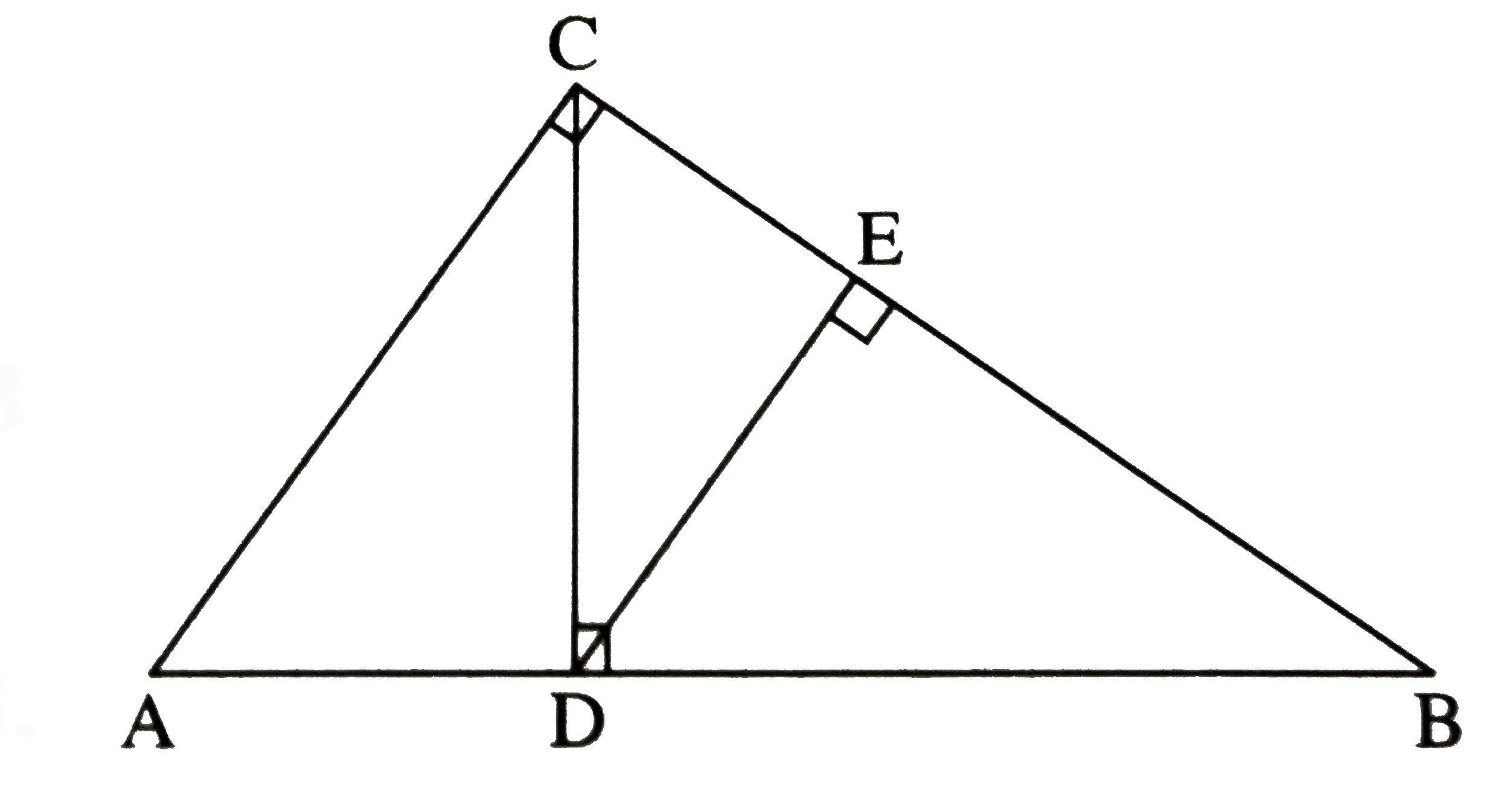
View SolutionIn △ ABC ,
∠ACB=90∘ ,
CD⊥AB and
DE⊥CB
Prove that CD2×AC=AD×AB×DE .
View SolutionABC is a triangle in which AB=AC and D is any point in BC . Prove that AB2−AD2=BDCD .
View Solution
