ABCD is a trapezium in which AB || DCand P, Qare points on AD and BC respectively, such that PQ II DC. If PD - 18 cm, BQ = 35 cm and QC = 15 cm, then find the length of AD.
To find the length of AD in trapezium ABCD where AB || DC, and PQ is parallel to DC, we can follow these steps:
Step 1: Understand the given information
We have a trapezium ABCD with:
- AB || DC
- Points P and Q on sides AD and BC respectively such that PQ || DC
- PD = 18 cm
- BQ = 35 cm
- QC = 15 cm
Step 2: Use the Basic Proportionality Theorem
Since PQ is parallel to DC, we can apply the Basic Proportionality Theorem (also known as Thales' theorem). This theorem states that if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
Step 3: Set up the ratios
For triangle ABD:
- Let AP = x
- According to the theorem, we have:
PDAP=ABBD(1)
For triangle ABC:
- Let OB = y
- We can write:
BQQC=OBOD(2)
Step 4: Relate the two triangles
From the two triangles ABD and ABC, we can relate the segments:
- From (1):
18x=ABBD
- From (2):
3515=yOD
Since both equations involve the same segments, we can equate them:
PDAP=QCBQ
This gives us:
18x=1535
Step 5: Solve for x (AP)
Cross-multiplying gives:
18⋅35=15⋅x
Calculating the left side:
630=15x
Now, divide both sides by 15:
x=63015=42 cm
Step 6: Find the length of AD
Now we can find AD:
AD=AP+PD
Substituting the values we found:
AD=42+18=60 cm
Final Answer
The length of AD is 60 cm.
---
We have a trapezium ABCD with:
- AB || DC
- Points P and Q on sides AD and BC respectively such that PQ || DC
- PD = 18 cm
- BQ = 35 cm
- QC = 15 cm
Since PQ is parallel to DC, we can apply the Basic Proportionality Theorem (also known as Thales' theorem). This theorem states that if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
For triangle ABD:
- Let AP = x
- According to the theorem, we have:
PDAP=ABBD(1)
- Let OB = y
- We can write:
BQQC=OBOD(2)
From the two triangles ABD and ABC, we can relate the segments:
- From (1):
18x=ABBD
- From (2):
3515=yOD
PDAP=QCBQ
This gives us:
18x=1535
Cross-multiplying gives:
18⋅35=15⋅x
Calculating the left side:
630=15x
Now, divide both sides by 15:
x=63015=42 cm
Now we can find AD:
AD=AP+PD
Substituting the values we found:
AD=42+18=60 cm
The length of AD is 60 cm.
Topper's Solved these Questions
- SAMPLE PAPER 12 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 12 EXERCISE - PART - B (SECTION -IV)
9 Videos
- SAMPLE PAPER - 6 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER - 6 EXERCISE - PART - B (SECTION - IV)
13 Videos
- SAMPLE PAPER 5 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5 EXERCISE - Part B (Section - V)
4 Videos
Similar Questions
ABCD is a trapezium in which AB||DC and P,Q are points on AD and BC respectively, such that PQ||DC, if PD=18 cm, BQ=35 cm and QC=15 cm. Find AD.
View SolutionABCD is a trapezium in which ABIIDC and P and Qare points on AD and BC respectively such that PQ||DC. If PD= 12 cm, BQ = 42 cm and QC = 18cm, find AD.
View Solution
Knowledge Check
In ΔABC D and E are the points on sides AB and AC, respectively, such that DE || BC. If AD = 4 cm, BC = 5 cm. DC = 10 cm and AB = 15 cm. then the sum of the lengths of DE and EC is:
AA. 20 cmBB. 15 cmCC. 21 cmDD. 18 cmABCD is a trapizium with AB∣∣DC. E and F are points on non - parallel sides AD and BC respecitively such that EF∣∣AB, If AE = 3cm, ED = 4.8 cm, BF = 1.5 cm, then the value of CF is :
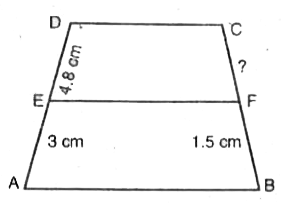 A4.5 cmB2.4 cmC6.0 cmDNone of these
A4.5 cmB2.4 cmC6.0 cmDNone of theseQuadrilateral ABCD circumscribes a circle. If AB = 8 cm, BC = 7 cm and CD = 6 cm, then the length of AD is:
A7 cmB6.8 cmC7.5 cmD6 cm
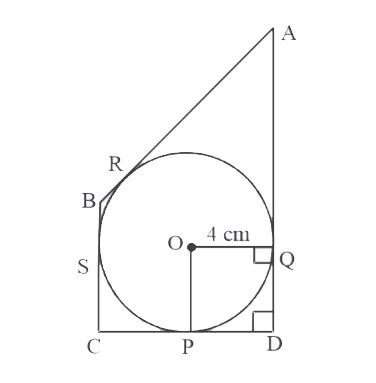
In the given fig., find PC. If AB = 13 cm, BC = 7 cm and AD = 15 cm.
View SolutionIf DE||BC in △ABC where D and E are points on AB and AC respectively. If ADDB=815 and EC = 3.5 cm , find AE.
View SolutionABCD is a trapezium of sides in which BC || AB & AB=9cm, BC=12cm, CD=15cm & DA=20cm. Find the sum of square of its diagonal.
View SolutionABCD is a trapezium such that AB, DC is parallel and BC is perpendicular to them. If angle (DAB) = 45∘ , BC = 2 cm and CD = 3 cm, then find the length of AB?
View SolutionABCD is a trapezium in which AB || DC a and DC= 40 cm and AB = 60 cm. If X and Y a re respectively, the midpoints of AD and BC, then

XY=
View Solution
