The radius of curvature of each surface of a lens is 40 cm. Its refractive index is 1.5. The focal length of lens will be
40 cm
20 cm
80 cm
30 cm
The correct Answer is:A
For a lens, 1f=(aμg−1)(1R1−1R2)
1f=(15−1)(1R+1R)=(0.5)×2R=1R
f=R=40 cm
Similar Questions
The radius of curvature of curved surface of a thin plano-convex lens is 10cm and the refractive index is 1.5. If the plano surface is silvered, then the focal length will be.
View SolutionThe radius curvature of each surface of a convex lens of refractive index 1.5 is 40 cm. Calculate its power.
View Solution
Knowledge Check
The radius of curvature for a convex lens is 40 cm , for each surface. Its refractive index is 1.5. The focal length will be
A40 cmB20 cmC80 cmD30 cmThe radius of curvature of curved surface of a thin plano-convex lens is 10cm and the refractive index is 1.5. If the plano surface is silvered, then the focal length will be.
A15 cmB20 cmC5 cmD10 cmThe radius curvature of each surface of a convex lens of refractive index 1.5 is 40 cm. Calculate its power.
A2.5DB2DC1.5DD1D
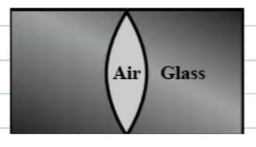
In figure, an air lens of radius of curvature of each surface equal to 10cm is cut into a cylinder of glass of refractive index 1.5. The focal length and the nature of lens are

View SolutionThe radius of curvature of the face of plano-convex lens is 12cm and its refractive index is 1.5. If the plane surface of the lens is now silvered, then find the focal length of the lens.
View SolutionThe radius of curvature of the curved surface of a plano-convex lens is 20cm. If the refractive index of the material of the lens be 1.5, it will
View SolutionThe radius of curvature of the curved surface of a plano-convex lens is 20cm. If the refractive index of the material of the lens be 1.5, it will
View SolutionIn figure, an air lens of radius of curvature of each surface equal to 10cm is cut into a cylinder of glass of refractive index 1.5. The focal length and the nature of lens are
View Solution