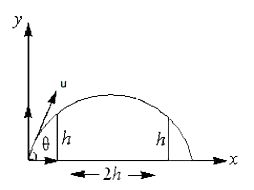
A particle is projected with
velocity 2√gh. What will be
the time interval for a particle
to cross two walls of equal
height h separated by a
distance of 2h from each other ?
2hg
√2hg
√hg
2√hg
The correct Answer is:D
Let t be the time interval. Then,
2h=(ux)(t)
or ux=2ht.....(i)
Further, h=uyt−12gt2
or gt2−2uyt+2h=0
t1=2uy+√4u2y−8gh2g
and t2=2uy−√4u2y−8gh2g
t=t1−t2=√4u2y−8ghg
or u2y=g2(t)24+2gh
Given, u2x+u2y=(2√gh)2
4h2(t)2+g2(t)24+2gh=4gh
g24(t)4−2gh(t)2+4h2=0
(Δt)2=2gh±√4g22h−4g22hg2/2=4hg
or Δt=2√hg
Topper's Solved these Questions
- NTA TPC JEE MAIN TEST 30BOOK - NTA MOCK TESTSCHAPTER - NTA TPC JEE MAIN TEST 30EXERCISE - PHYSICS (SUBJECTIVE NUMERICAL)
10 Videos
- NTA TPC JEE MAIN TEST 124 BOOK - NTA MOCK TESTSCHAPTER - NTA TPC JEE MAIN TEST 124 EXERCISE - PHYSICS
30 Videos
- NTA TPC JEE MAIN TEST 36BOOK - NTA MOCK TESTSCHAPTER - NTA TPC JEE MAIN TEST 36EXERCISE - PHYSICS
30 Videos
Similar Questions
A particle is projected with velocity 2√gh so that it just clears two walls of equal height h which are at a distance 2h from each other. Show that the time of passing between the walls is 2√h/g.
View SolutionA particle is projected with velocity 2√gh so that it just clears two walls of equal height h which are at a distance 2h from each other. Show that the time of passing between the walls is 2√h/g.
View Solution
Knowledge Check
A particle is projected with velocity 2√gh so that it just clears two walls of equal height h which are at a distance 2h from each other. Show that the time of passing between the walls is 2√h/g.
A2hgB√2hgC√hgD2√hgA particle is projected with velocity 2√gh so that it just clears two walls of equal height h which are at a distance 2h from each other. Show that the time of passing between the walls is 2√h/g.
A√hgB√2hgC2√hgD2hg
A particle is projected with velocity 2√(ag) so that it just clears two walls of equal height a, which are at a distance 2a from each other. The latus rectum of the path is 2a and the time of passing between the walls is 2√ag
View SolutionA particle is projected with velocity 2√ag so that it just clears two walls, of equal height a, at a distance 2a from each other . Show that the velocity of projection is 60∘ and that the latus rectum of the path is 2a.
View SolutionA particle is projected with a velocity u from a point at ground level. Show that it cannot clear a wall of height h at a distance x from the point of projection if u2<g(h+√h2+x2).
View SolutionA particle is projected from the ground at t=0 so that on its way it just clears two vertical walls of equal height on the ground. The particle was projected with initial velocity u and at angle θ with the horiozontal. If the particle passes just grazing top of the wall at time t=t1andt=t2, then calculate.
(a) the height of the wall.
(b) the time t1andt2 in terms of height of the wall.
Write the expression for calculating the range of this projectile and separation between the walls.
View SolutionA particle is projected from the ground at t=0 so that on its way it just clears two vertical walls of equal height on the ground. The particle was projected with initial velocity u and at angle θ with the horiozontal. If the particle passes just grazing top of the wall at time t=t1andt=t2, then calculate.
(a) the height of the wall.
(b) the time t1andt2 in terms of height of the wall.
Write the expression for calculating the range of this projectile and separation between the walls.
View SolutionA particle is projected from ground with velocity 20(√2)m/s at 45∘. At what time particle is at height 15 m from ground? (g=10m/s2)
View Solution
