Question

Two particles A and B have masses 3 kg and 6 kg and velocities 8 m/s and 6 m/s respectively. They collide elastically at the origin with their velocities making angles ${45}^{\circ }$ and ${120}^{\circ }$ respectively with positive y - axis at that instant. Find the velocity of particle B after the collision. (Take $\sqrt{2}=1.41\text{and}\sqrt{3}=1.73$)

Answer

`11.47`

Explanation

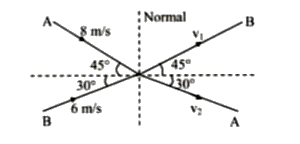
Applying law of conservation of linear momentum in X and Y direction of the system,
`3 (8 cos 45^(@)) +6(6 cos 30^(@) ) = 6 (v_(1) cos45^(@)) + 3 (v_(2) cos 30^(@))`
`12 sqrt(2) +18 sqrt(3) = v_(1) 3 sqrt(2) +"v"_(2) (3sqrt(3))/(2)`
`:. 3 sqrt(2) v_(1) +(3sqrt(3))/(2) v_(2) = 48.06 ...(i)`
Also,
`6(6 sin 30^(@)) - 3 (8 sin 45^(@)) = 6(v_(1) sin 45^(@)) - 3(v_(2) sin 30^(@))`
`:.18 -12 sqrt(2) =3 sqrt(2) v_(1) -(3)/(2) v_(2)`
`:.3 sqrt(2)v_(1) -(3)/(2) v_(2) = 1.08 ...(ii)`
On solving equation (i) and (ii), we get,
`(3)/(2) (sqrt(3) +1) v_(2) =46.98`
`v_(2) = (46.98 xx 2)/(3xx 2.73)`
`:.v_(2) = 11.47 m//s`