An infinite ladder network is constructed with 1Ωand 2Ω resistors as shown. Find the equivalent resistance points A and B. 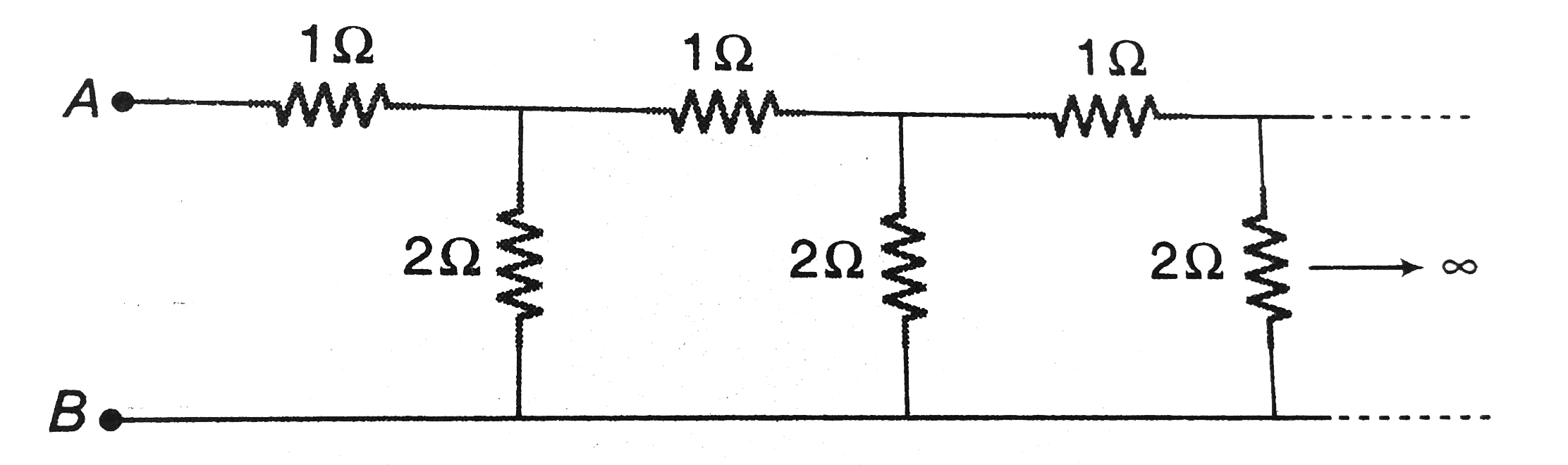
1Ω
2Ω
3Ω
5/8Ω
The correct Answer is:B
x=2xx+2+1
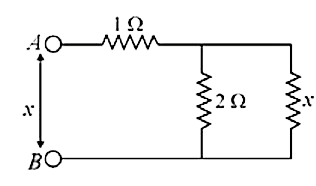
x2+2x=2x+x+2
x2−x−2=0
(x−2)(x+1)=0
x=2Ω
Topper's Solved these Questions
- NTA TPC JEE MAIN TEST 47BOOK - NTA MOCK TESTSCHAPTER - NTA TPC JEE MAIN TEST 47EXERCISE - PHYSICS (SUBJECTIVE NUMERICAL)
10 Videos
- NTA TPC JEE MAIN TEST 46BOOK - NTA MOCK TESTSCHAPTER - NTA TPC JEE MAIN TEST 46EXERCISE - PHYSICS
30 Videos
- NTA TPC JEE MAIN TEST 48BOOK - NTA MOCK TESTSCHAPTER - NTA TPC JEE MAIN TEST 48EXERCISE - PHYSICS
29 Videos
Similar Questions
An infinite ladder is constructed with 1Ωand2Ω resistors as shown in Fig 27-49. Find the effective resistance between the points A and B.
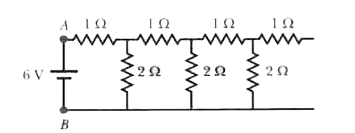
View SolutionAn infinite ladder is constructed with 1(Ω)and 2(Ω)resistor as shown in figure.(a)Find the effective resistance between the point A and B. (b) Find the current that passes through the (2Ω) resistor nearest to the battery.

View Solution
Knowledge Check
The figure shows a network of resistor each having value 12Ω. Find the equivalent resistance between points A and B.
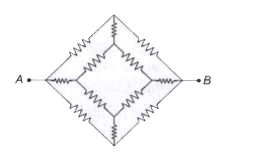 A9ΩB125ΩC8ΩD113Ω
A9ΩB125ΩC8ΩD113ΩAn infinite ladder network is arranged with resistances R and 2 R as shown. The effective resistance between terminals A and B is
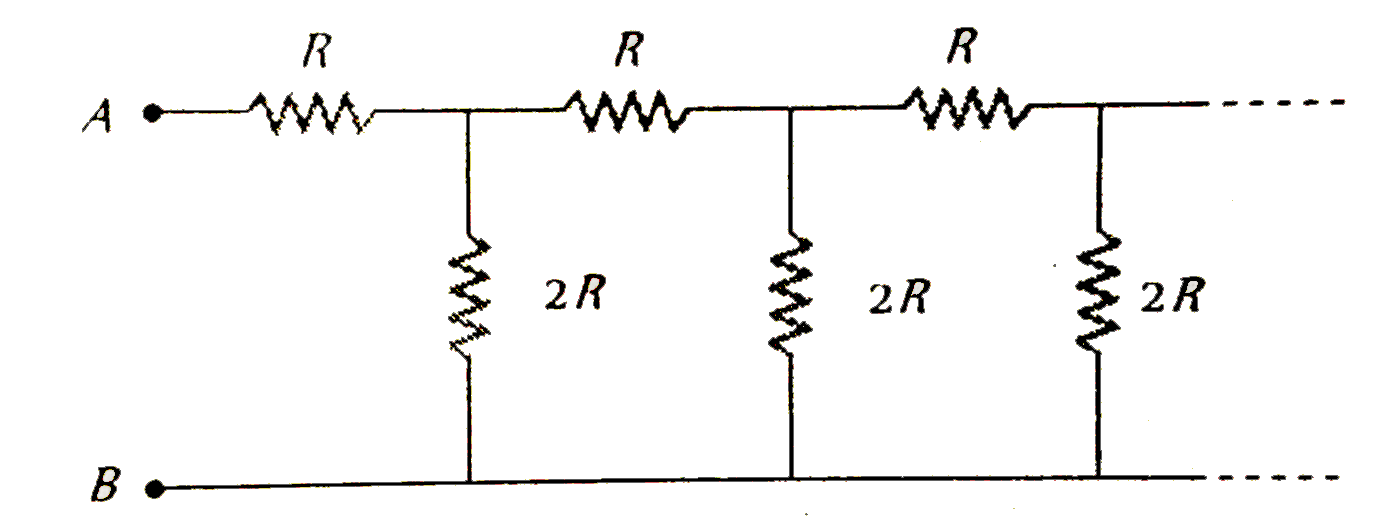 A∞BRC2RD3R
A∞BRC2RD3RThe figure shows a network of resistor each heaving value 12Ω. Find the equivalent resistance between points A and B.
 A9ΩB125ΩC8ΩD113Ω
A9ΩB125ΩC8ΩD113Ω
The network of resistors. Find the equivalent resistance between points A and D.
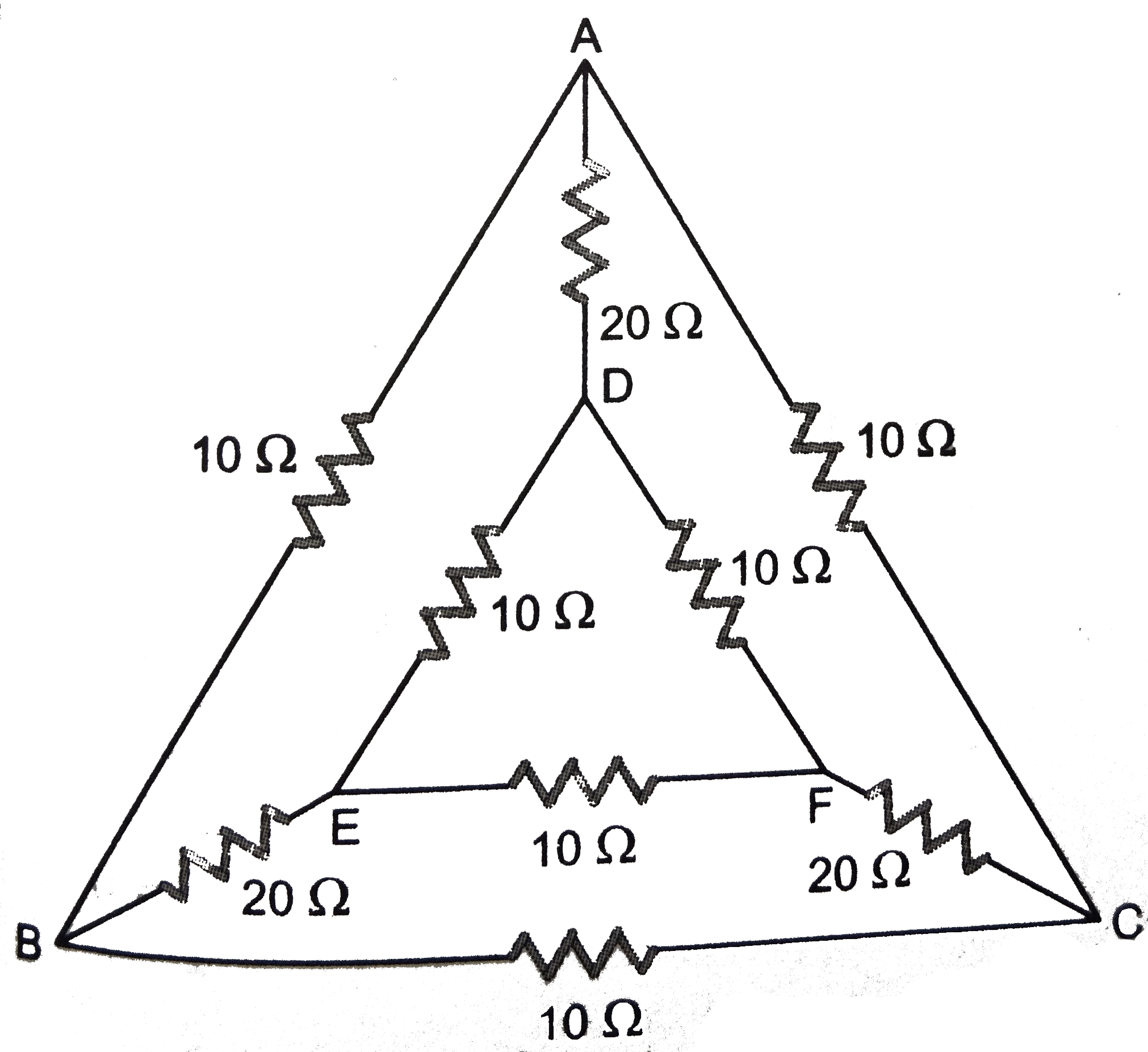
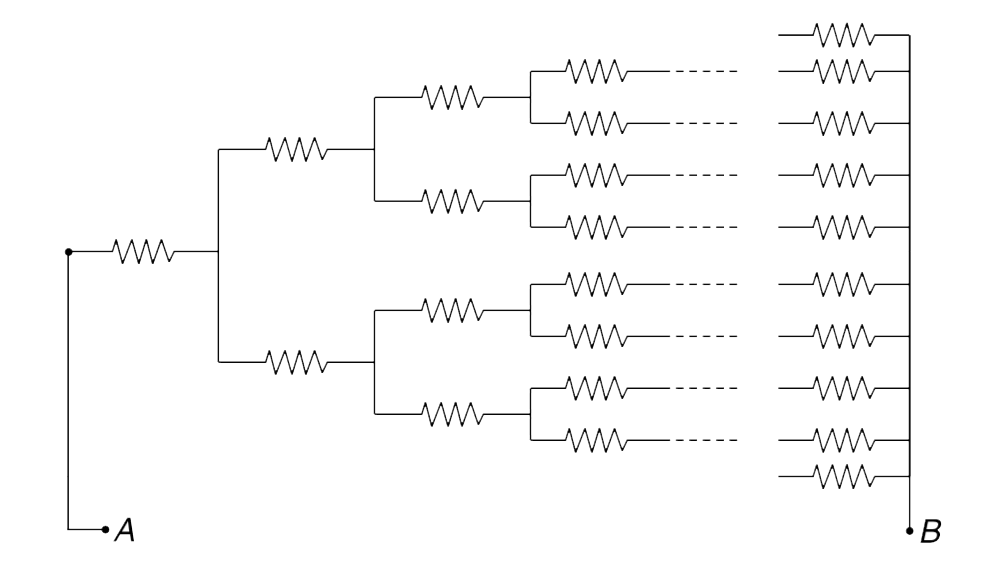
View SolutionAn infinite network of resistances has been made as shown in the figure. Each resistance is R. find the equivalent resistance between A and B.
View SolutionEach resistance is of 1Ω in the circuit diagram shown in figure. Find out equivalent resistance between A and B.
View SolutionIn the network of resistors shown in the adjoining figure, the equivalent resistance between A and B is

View SolutionFor infinite ladder network containing identical resistance of RΩ each, are combined as shown in figure. The equivalent resistance between A and B is RAB and between A and C is RAC. Then the value RABRAC is :

View Solution
