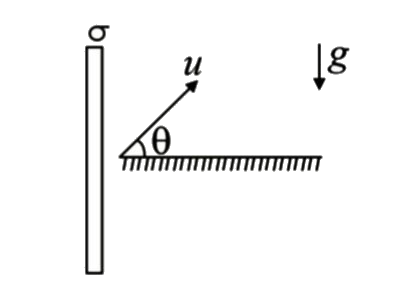
In the set-up shown, there is a large thin non-conducting vertical sheet with charge density σ. In the nearby region a charge q of mass m is projected at an angle θ with initial velocity u. When this charge reaches its maximum height, find its velocity.
ucosθ(1+σqtanθ2mε0p)
ucosθ(1+σqtanθmε0p)
usinθ(1+σqtanθ2mε0p)
usinθ(1+σqtanθmε0p)
The correct Answer is:A
Fy=mg(−ˆj)Fx=(σ2ε0)q(ˆi)
ay=−g(ˆj)ax=(σqm2ε0)ˆi
At Sy=Hmax,Vy=0
Let the time taken to reach max. height be t1
vy=uy+ayt1
⇒0=usinθ−gt1
⇒t1=usinθg
At t=t1,vx=ux+axt1
⇒vx=ucosθ+(σq2mε0)usinθg
−ucosθ[1+σqtanθ2mε0g]
Topper's Solved these Questions
Similar Questions
In the figure shown there is a large sheet of charge of uniform surface charge density'σ'.A charge particle of charge '−q' and mass 'm' is projected from a point A on the sheet with a speed 'u' with the angle of projection such that it lands at maximum distance from A on the sheet. Neglecting gravity, find the time flight

View SolutionIn the figure shown, S is a large non-conducting sheet of uniform charge density σ. A rod R of length I and mass m is parallel to the sheet and hinged at its midpoint. The linear charge densities on the upper and lower half of the rod are shown in the figure. The angular acceleration of the rod just after it is released is pσλqmɛo. Find pq.
'(##CEN_KSR_PHY_JEE_C18_E01_031_Q16##)'
View Solution
Knowledge Check
In the figure shown there is a large sheet of charge of uniform surface charge density'σ'.A charge particle of charge '−q' and mass 'm' is projected from a point A on the sheet with a speed 'u' with the angle of projection such that it lands at maximum distance from A on the sheet. Neglecting gravity, find the time flight
 A2√2mvε0σqB√2mvε05σqCmvε0√2σqDmvε02√2σq
A2√2mvε0σqB√2mvε05σqCmvε0√2σqDmvε02√2σq
A body is projected vertically up with u. Its velocity at half its maximum height is
View SolutionA body is projected vertically up with a valocity u. its velocity at ghalf of its maximum height and at 3/4th of its maximum height are.
View SolutionIn the figure shown S is a large nonconducting sheet of uniform charge density σ. A rod R of length l and mass 'm' is parallel to the sheet and hinged at its mid point. The linear charge densities on the upper and lower half of the rod are shown in the figure. Find the angular acceleration of the rod just after it is released.
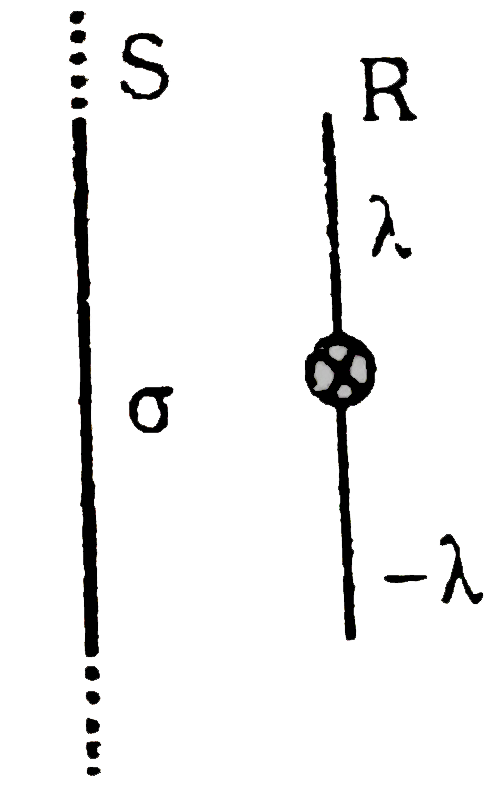
View SolutionA body is projected vertically up from ground with a velocity u so as to reach maximum height 'h'. At half of the maximum height its velocity will be
View SolutionA particle is projected with velocity u at angle θ with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.
View SolutionA particle is projected with velocity u at angle θ with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.
View SolutionA particle is projected with velocity u at angle θ with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.
View Solution
