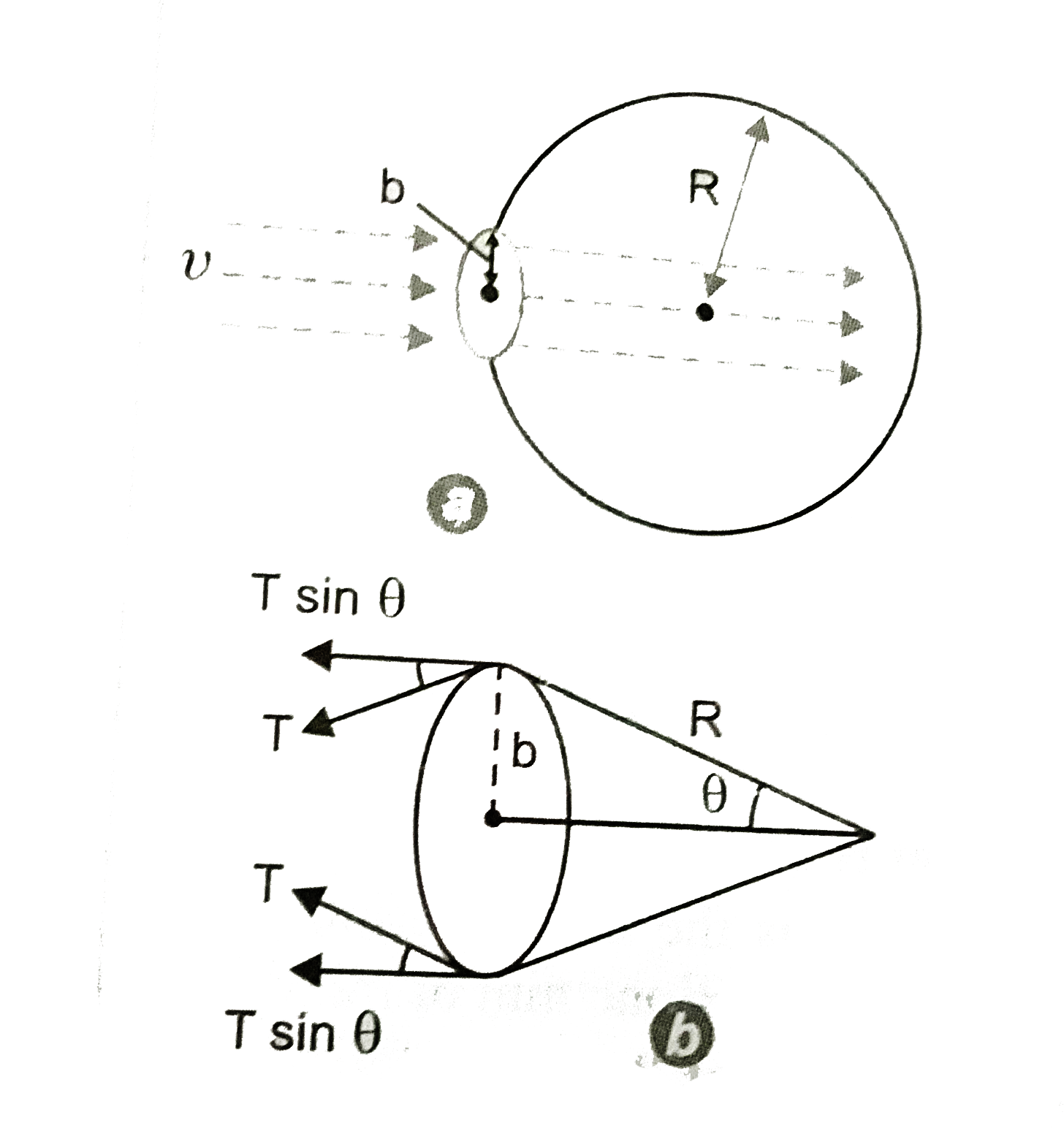
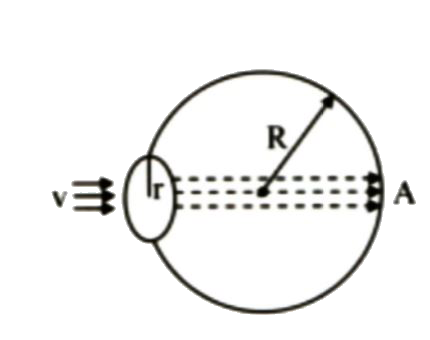
A bubble having surface tension T and radius R is formed on a ring of radius b $(b < > R)$ . Air is blown inside the tube held in front of the ring , with velocity $υ$ as shown in fig. The air molecules collides perpendicularly with the wall of the bubble and stops. Calculate the radius R at which the bubble and stops. Calculate the radius R at which the bubble separates from the ring.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $04.00$

Excess pressure inside a bubble $= \frac{4 T}{R}$
Let area of wall of bubble where air strikes be A.

$∴$ Force due to excess pressure $= \frac{4 T A}{R}$
Now, force due to striking air $= ρ A v^{2}$
For bubble to separate from the ring.
$p A v^{2} = \frac{4 T A}{R} \Rightarrow R = \frac{4 T}{ρ v^{2}}$
$\Rightarrow Z = 4$

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

The excess pressure inside a soap bubble P and the radius R of the bubble are related as
A $p \propto 1 / R$
B $P \propto R$
C $P \propto R^{2}$
D $P \propto 1 / R^{2}$
The surface tension of soap is T . The work done in blowing a soap bubble of radius 3 R to that of a radius 5R is
A $64 π R^{2} T$
B $100 π R^{2} T$
C $128 π R^{2} T$
D $256 π R^{2} T$
A soap bubble of radius $r$ is placed on another bubble of radius $2 r$ . The radius of the surface common to both the bubbles is
A $\frac{2 r}{3}$
B $3 r$
C $2 r$
D $r$

NTA MOCK TESTS-NTA TPC JEE MAIN TEST 51-PHYSICS

Home
Ask Doubt
Profile