In the figure, two straight conducting rails form a right angle. A conducting bar in contact with the rails starts at the vertex at time t= 0 and moves with a constant velocity of v along them. A magnetic field B is directed out of the page. The current in the loop is (λ = resistance per unit length of the rails and bar).
2BVλ
BVλ(1+√2)
√2Bvλ
2Bvλ(1+√2)
The correct Answer is:B
EMF=ddt(Bvt×vt)=2Bv2t
and resistance =λ(2vt+2√2vt)
Topper's Solved these Questions
- NTA TPC JEE MAIN TEST 55BOOK - NTA MOCK TESTSCHAPTER - NTA TPC JEE MAIN TEST 55EXERCISE - PHYSICS (SUBJECTIVE NUMERICAL)
10 Videos
- NTA TPC JEE MAIN TEST 54BOOK - NTA MOCK TESTSCHAPTER - NTA TPC JEE MAIN TEST 54EXERCISE - PHYSICS
30 Videos
- NTA TPC JEE MAIN TEST 56BOOK - NTA MOCK TESTSCHAPTER - NTA TPC JEE MAIN TEST 56EXERCISE - PHYSICS
30 Videos
Similar Questions
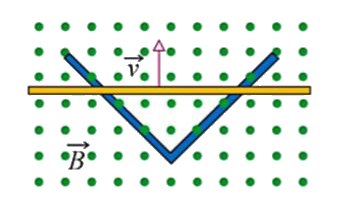
Two straight conducting rails form a right angle where their ends are joined. A conducting bar in contact with the rails starts at the vertex at time t = 0 and moves with constant velocity v along them as shown in Fig. A magnetic field →B is directed into the page. the induced emf in the circuit at any time t is proportional to

View SolutionTwo straight conducting rails form a right angle where their ends are joined. A conducting bar in contact with the rails starts at the vertex at time t = 0 and moves with constant velocity v along them as shown in Fig. A magnetic field →B is directed into the page. the induced emf in the circuit at any time t is proportional to

View Solution
Knowledge Check
Two straight conducting rails form a right angle where their ends are joined. A conducting bar in contact with the rails starts at the vertex at time t = 0 and moves with constant velocity v along them as shown in Fig. A magnetic field →B is directed into the page. the induced emf in the circuit at any time t is proportional to
 At∘BtCvoltage across L is equal to zero.Dv2
At∘BtCvoltage across L is equal to zero.Dv2A long conducting wire AH is moved over a conducting triangular wire CDE with a constant velocity v in a uniform magnetic field →B directed into the plane of the paper. Resistance per unit length of each wire is ρ. Then
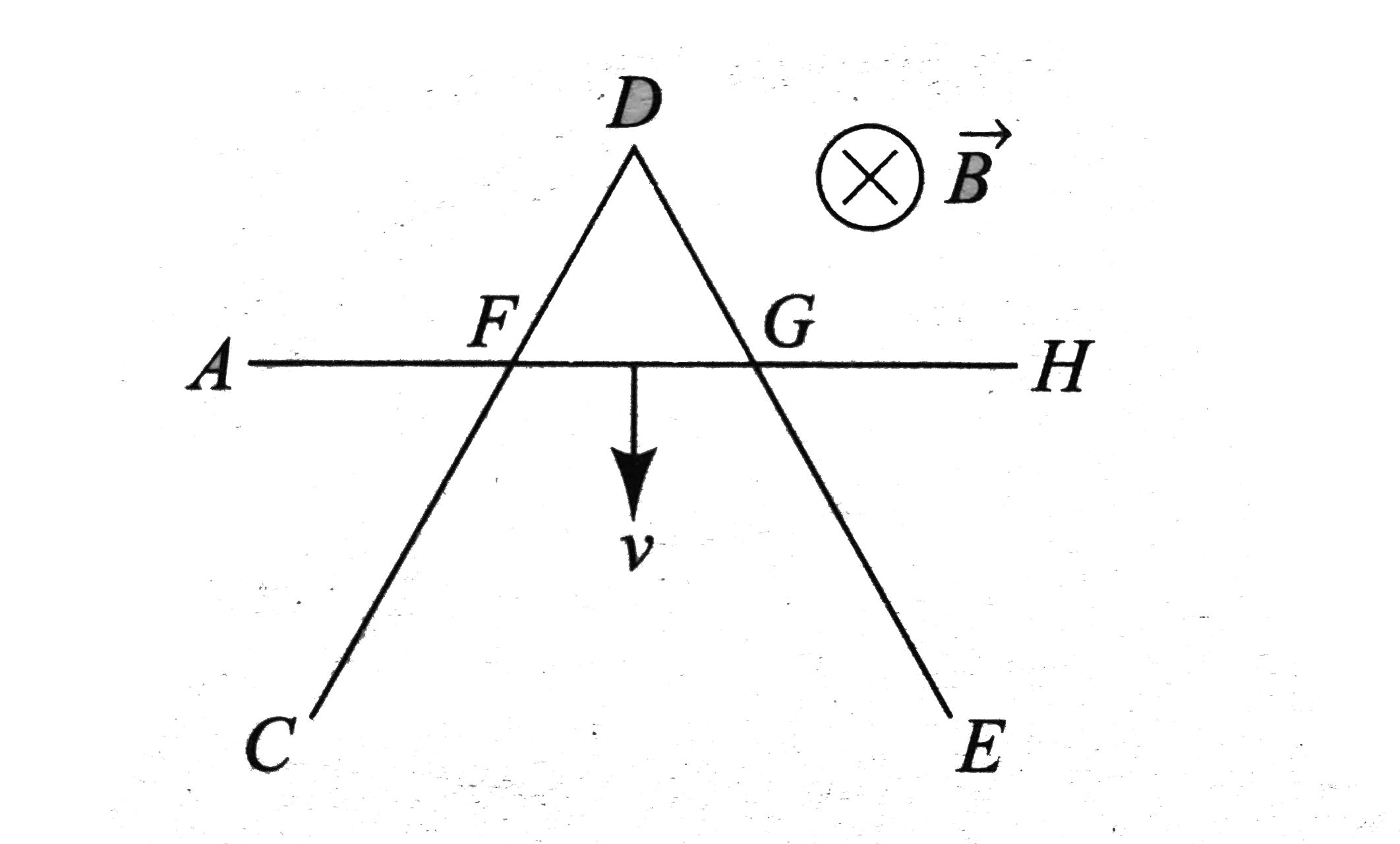 A(a) a constant clockwise induced will flow in the closed loopB(b) an increasing anticlockwise induced current will flow in the closed loopC(c ) a decreasing anticlockwise induced current will flow in the closed loopD(d) an constant anticlockwise induced current will flow in the closed loop
A(a) a constant clockwise induced will flow in the closed loopB(b) an increasing anticlockwise induced current will flow in the closed loopC(c ) a decreasing anticlockwise induced current will flow in the closed loopD(d) an constant anticlockwise induced current will flow in the closed loopTwo parallel long straight conductors lie on a smooth plane surface. Two other parallel conductors rest on them at right angle so as to form a square of side a. A uniform magnetic field B exists at right angle to the plane containing the conductors. Now, conductors starts moving outward with a constant velocity v0 at t=0. Then, induced current in the loop at any time is (λ is resistance per unit length of the conductors)
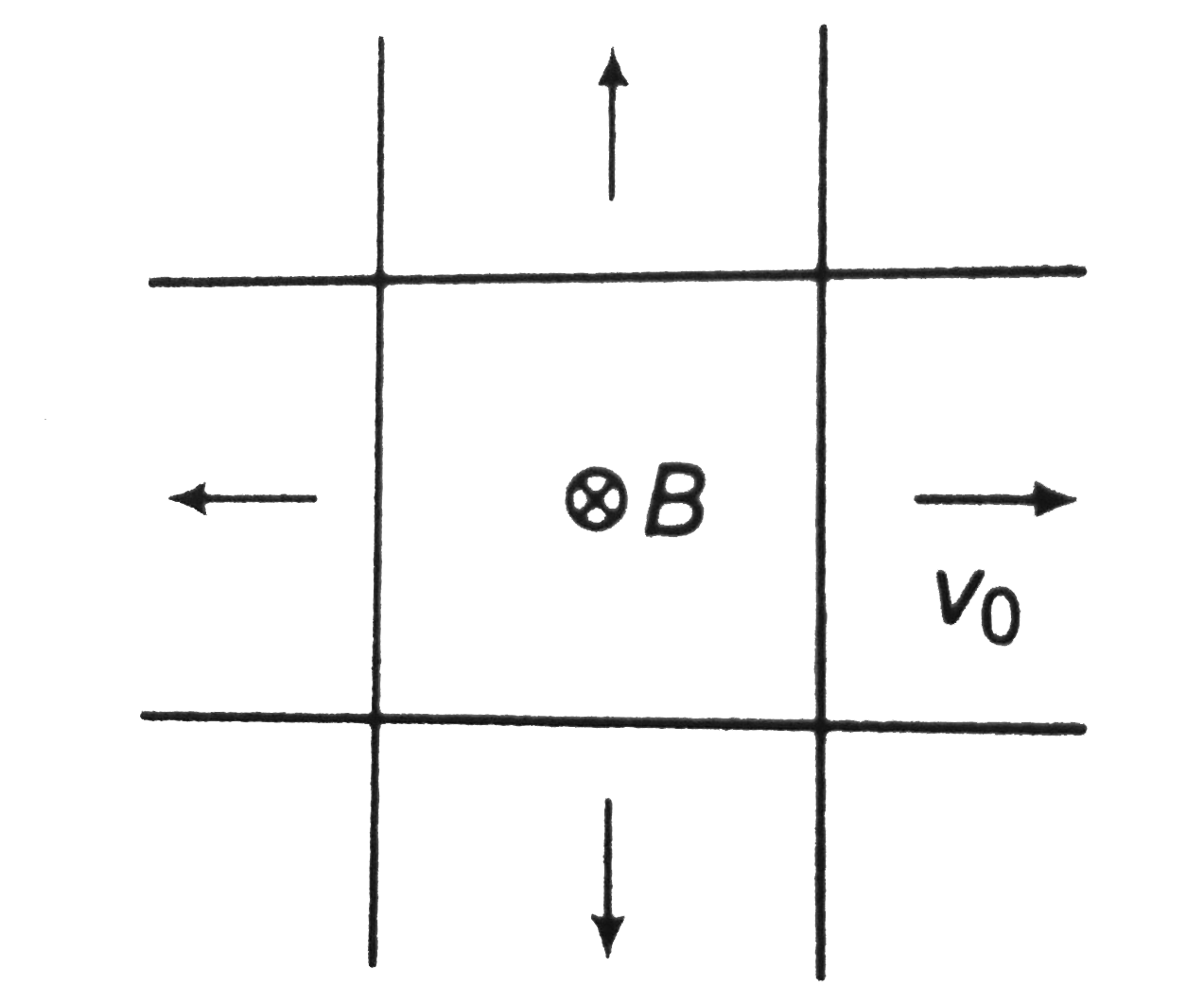 AaBv0λ(a+v0t)BaBv02λCBv0λDBv02λ
AaBv0λ(a+v0t)BaBv02λCBv0λDBv02λ
Two straight conducting rails form a right angle where their ands are joined. A conducting bar contanct with the rails starts at vertex at the time t=0 & moves symmetrically with a constant velocity of 5.2m/s to the right as shown in figure. A 0.35T magnetic field point out of the page. Calculate:
(i) The flux through the tringle by the rails & ber at t=3.0s.
(ii) The emf around the tringle at that time.
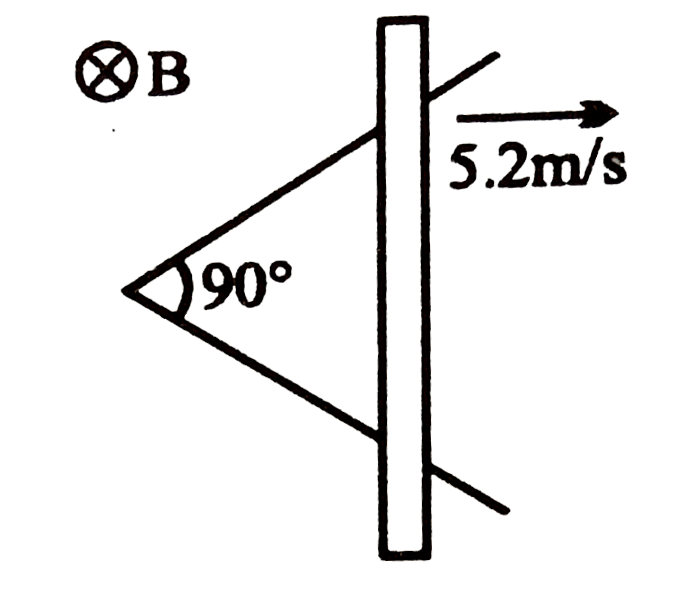
In what manner does the emf around the tringle vary with time.
View SolutionTwo straight conducting rails from a right angle where their end are joined. A conducting bar polaced over the rails starts at vertex at the time t=0 and moves with a constant velocity v to the right as shown in the figure. Calculate
(a) the flux through the triangle (isosceles) by the rails and bar at t=t0
the emf around the triangle at that time
(c) in what manner does the emf around the triangle vary with time
View SolutionA long conducting wire AH is moved over a conducting triangular wire CDE with a constant velocity v in a uniform magnetic field →B directed into the plane of the paper. Resistance per unit length of each wire is ρ. Then

View SolutionTwo parallel long straight conductors lie on a smooth plane surface. Two other parallel conductors rest on them at right angle so as to form a square of side a. A uniform magnetic field B exists at right angle to the plane containing the conductors. Now, conductors starts moving outward witha constant velocity v0 at t=0. Then, induced current in the loop at any time is (λ is resistance per unit length of the conductors)

View SolutionA conducting circular loop of radius a and resistance per unit length R is moving with a constant velocity v0 , parallel to an infinite conducting wire carrying current i0. A conducting rod of length 2a is approaching the centre of the loop with a constant velocity v02 along the direction 2 of the current. At the instant t=0, the rod comes in contact with the loop at A and starts sliding on the loop with the constant velocity. Neglecting the resistance of the rod and the self-inductance of the circuit, find the following when the rod slides on the loop.

(a) The current through the rod when it is at a distance of (a2) from the point A of the loop.
(b) Force required to maintain the velocity of the rod at that instant.
View Solution
