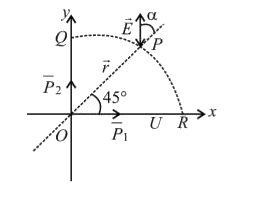
For a system of two dipoles →P1and→P2 as shown in the figure (both are at origin and perpendicular to each other along x and y-axes, respectively) (→P1and→P2) denotes magnetite of →P1and→P2 is quite large in comparison to dimensions of dipoles, →E is resultant electric field and QPR is a quarter of circle whose centre is at 0).
Work done in taking electron from P to R on QPR=0.
tanα=(P1+P2)2(P1−P2)
tanα=(P1−P2)2(P1+P2)
∫t=E.d→r=P1+P24√2πε0r2
The correct Answer is:B
For a system ……….
E1=2k(P1+P2)√2r3E32k(P1−P2)√2r3
tanα=E2E1
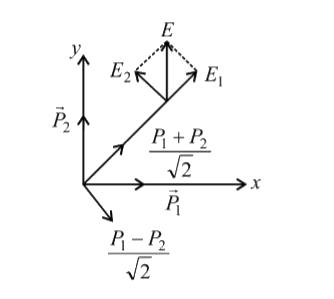
=P1−P22(P1+P2)
Topper's Solved these Questions
Similar Questions
If two vectors →P and →Q is chosen such that their resultant is perpendicular to →P . The angle between →P and →Q is cos−1(−nP2Q). Then value of n is:
View SolutionTwo dipoles →P1 and →P2 are oriented as shown in the figure. Assuming dipole of dipole moment →P2 to be placed at origin and dipole of moment →P1 is at a distance 'd' from origin then

View Solution
Knowledge Check
Two dipoles →P1 and →P2 are oriented as shown in the figure. Assuming dipole of dipole moment →P2 to be placed at origin and dipole of moment →P1 is at a distance 'd' from origin then
 ATorque experienced by →P1 is −18πε0P1P2d3ˆkBTorque experienced by →P1 is +14πε02P1P2d3ˆkCTorque experienced by →P1 is −14πε0P1P2d3ˆkDTorque experienced by →P1 is +14πε0P1P2d3ˆk
ATorque experienced by →P1 is −18πε0P1P2d3ˆkBTorque experienced by →P1 is +14πε02P1P2d3ˆkCTorque experienced by →P1 is −14πε0P1P2d3ˆkDTorque experienced by →P1 is +14πε0P1P2d3ˆkIf →P and →Q denote the sides of parallelogram and its area is 12PQ, then the angle between →P and →Qis
A0∘B30∘C45∘D60∘Vector →P angle α,β and γ with the x,y and z axes respectively.
Then sin2α+sin2β+sin2γ=A0B1C2D3
A point dipole →p=−p0xˆx is kept at the origin. The potential and electric field due to this dipole on the y-axis at a distance d are respectively (take V=0 at infinity)
View SolutionVector →P angle α,β and γ with the x,y and z axes respectively.
Then sin2α+sin2β+sin2γ=
View SolutionAssertion:- If dipole (→P1) is moved along the line normal to the axis (dotted line shown) of another dipole (→p2), their interaction energy does not chagne.

Reason:- Electric field of →p2 at the position of →p1 is normal to →p1.
View Solution→Pand→Q are two vectors having magnitude 1 and 3 respectively and inclined at an angle θ .
If ∣∣→P+→Q∣∣=√7, then find the value of (2→P+→Q).(→P−→Q)
View SolutionAssertion:- If dipole (→P1) is moved along the line normal to the axis (dotted line shown) of another dipole (→p2), their interaction energy does not chagne.

Reason:- Electric field of →p2 at the position of →p1 is normal to →p1.
View Solution
