A uniform magnetic field of induction B is confined to a cyclindrical region of radius R. The magnetic field is increasing at a constant rate of dB/dt (tesla/ second). A charge e of mass m, placed at the point P on the periphery of the fixed experiences an acceleration :
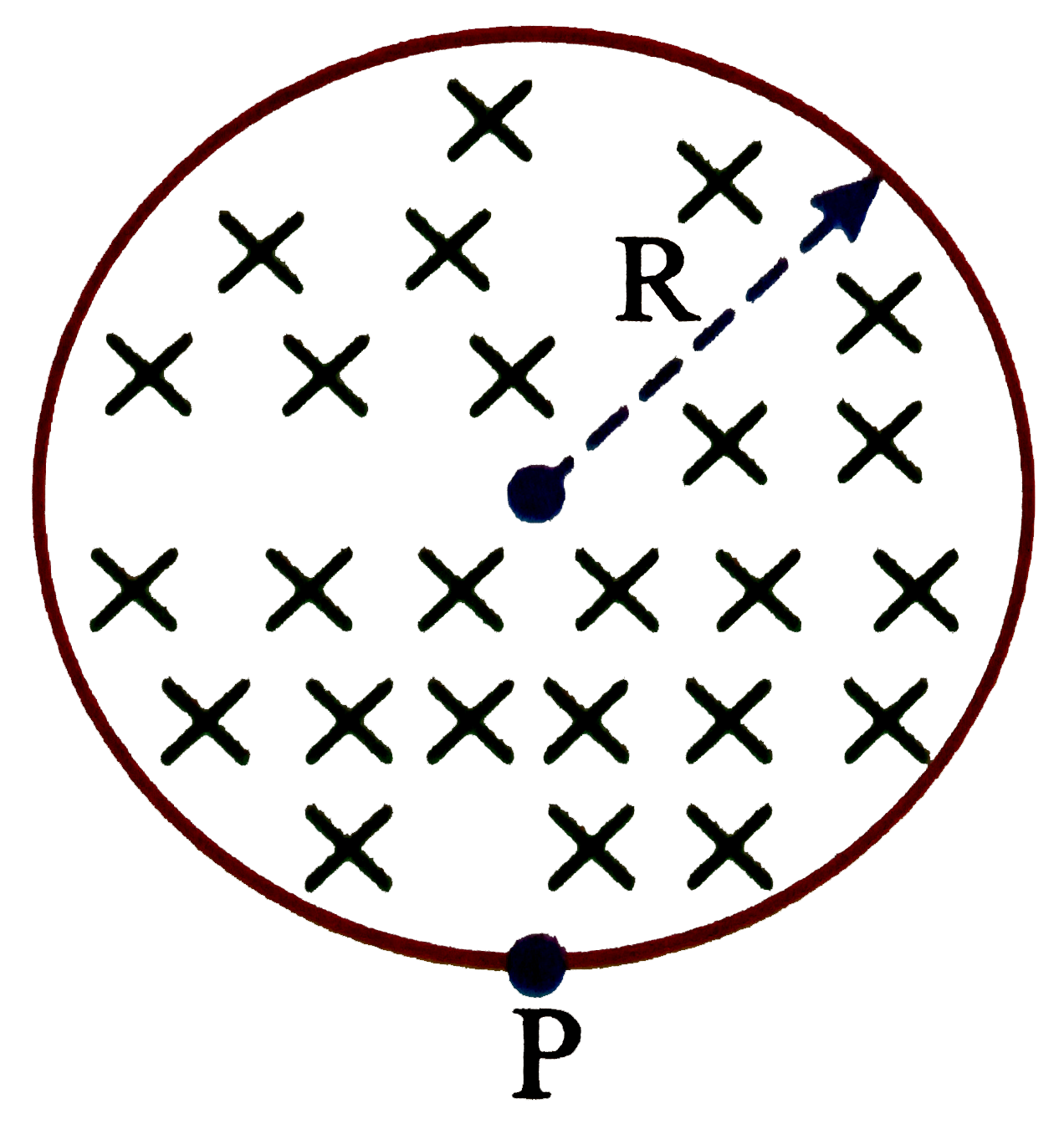
12eRmdBdt towards left
12eRmeBdt towards right
eRmdBdt towards left
zero
The correct Answer is:A
If we consider the cylindrical surface to be a ring of radius R, there will be an induced electric field due to time varying magnetic field.
∫→E.→dl=−dϕdt=AdBdt
⇒E(2πR)=AdBdt=πR2dBdt
E=R2dBdt
So force on the electron
F=−Ee=−eR2dBdt
Acceleration =12eRmdBdt
Force will be towards left on electron.
Topper's Solved these Questions
Similar Questions
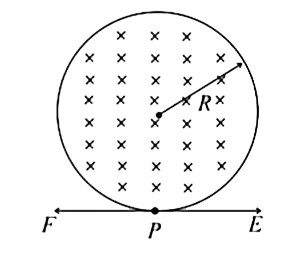
A uniform magentic field of induction B is confined in a cyclinderical region of radius R. If the field is incresing at a constant rate of dBdt=αT/s, then the intensity of the electric field induced at point P, distant r from the axis as shown in the figure is proportional to :
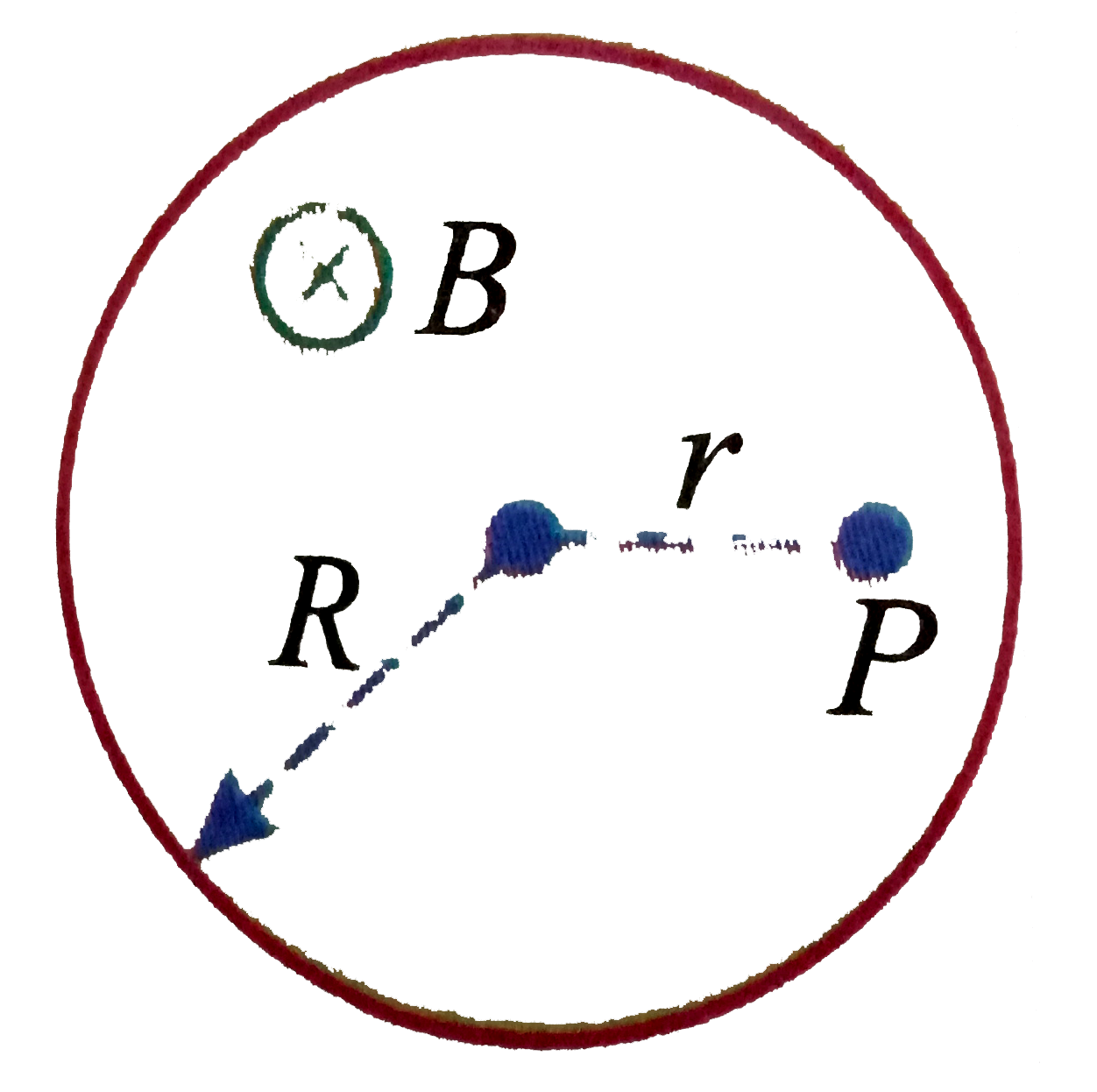
View SolutionFigure shows a uniform magnetic field of induction B confined to a cylindrical volume of radius R. B is increasing at a constant rate of 100 T/s. What is instantaneous acceleration experienced by a charged particle placed at C distant r from centre. Assume r = 5 m.
(Given qm=1.6×10−2 C/kg)
View Solution
Knowledge Check
A uniform magnetic field of induction B is confined to a cyclindrical region of radius R. The magnetic field is increasing at a constant rate of dB/dt (tesla/ second). A charge e of mass m, placed at the point P on the periphery of the fixed experiences an acceleration :
 A12eRmdBdt towards leftB12eRmeBdt towards rightCeRmdBdt towards leftDzero
A12eRmdBdt towards leftB12eRmeBdt towards rightCeRmdBdt towards leftDzeroFigure shown a uniform magnetic field B confined to a cylindrical volume and is increasing at a constant rate. The instantaneous acceleration experienced by an electron placed at P is
 Azero, since charge on electron in constantBtowards rightCtowards leftDupwords
Azero, since charge on electron in constantBtowards rightCtowards leftDupwordsa uniform magnetic field of induction B fills a cylinderical volume of radius R. A rod AB of length 2l is placed as shown in . If B changing at the rate dB/dt, the emf that is produced by the changing magnetic field and that acts between the ends of the rod is
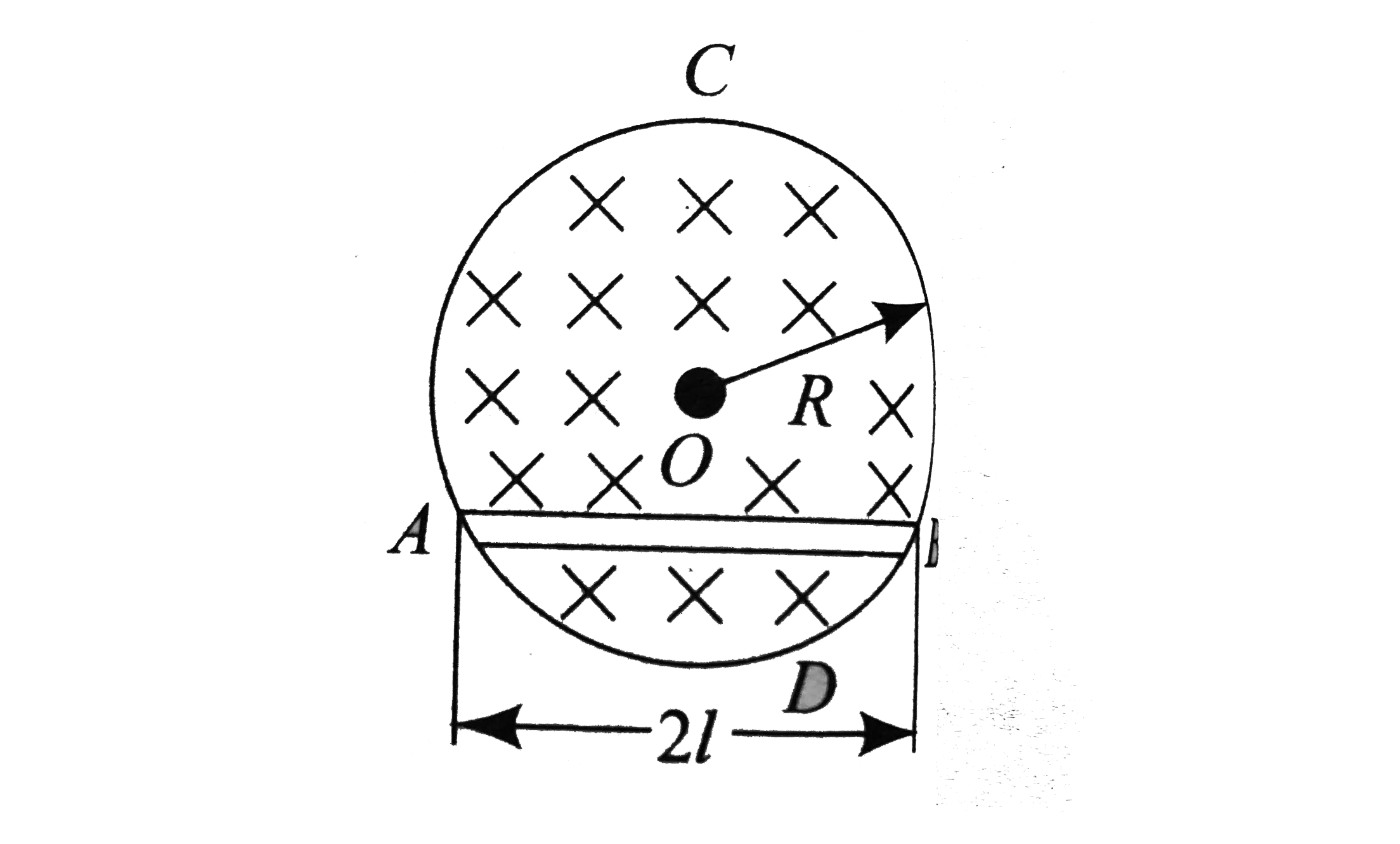 A(a) dBdtl√R2−l2B(b) dBdtl√R2+l2C( c) 12dBdtl√R2−l2D(d) 12dBdtl√R2+l2
A(a) dBdtl√R2−l2B(b) dBdtl√R2+l2C( c) 12dBdtl√R2−l2D(d) 12dBdtl√R2+l2
A uniform magnetic field B exists in a circular region of radius R. the field is perpendicular to the plane and is increasing at a constant rate of dBdt=α. There is a straight conducing rod AB of length 2R. Find the emf induced in the rod when it is placed as shown in figure (a) & (b). Point C is midpoint of the rod in figure (b)
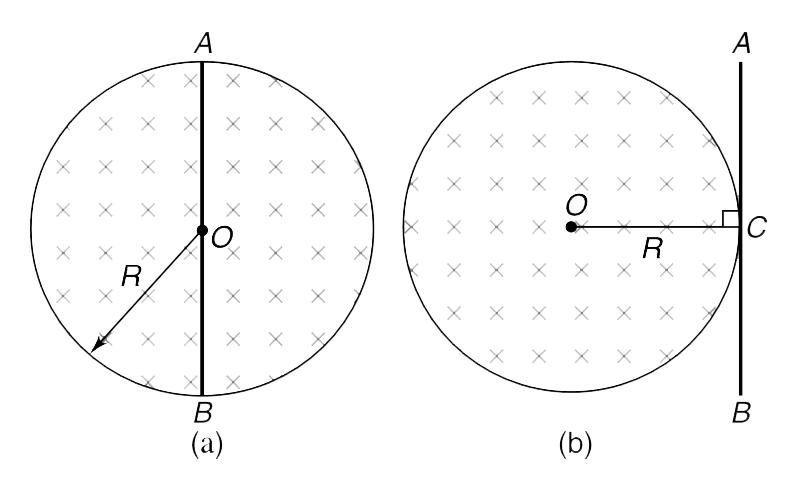
View SolutionThe magnetic field perpendicular to the plane of a conducting ring of radius r change ate the rate dBdt
View SolutionA charged particle of mass m is moving with a speed u in a circle of radius r. If the magnetic field induction at the centre is B, the charge on the particle is
View SolutionThe magnetic field within cylindrical region whose cross - section is indicated starts increasing at a constant rate α tesla/sec . The graph showing the variation of induced field with distance r from the axis of cylinder is :

View SolutionA uniform but time varying magnetic field is present in a circular region of radius R. The magnetic field is perpendicular and into the plane of the loop and the magnitude of field is increasing at a constant rate α. There is a straight conducting rod of length 2R placed as shown in figure.
The magnitude of induced emf across the rod is
View Solution
