Find the resultant amplitude of the following simple harmonic equations :
x1=5sinωt
x2=5sin(ωt+53∘)
x3=−10cosωt
A
5
B
10
C
15
D
20
Video Solution
Text Solution
The correct Answer is:B
x1=5sinωt
x2=5sin(ωt+53∘)
x3=−10cosωt
we can write
x3=10sin(ωt−90∘) Finding the resultant amplitude by vector notation.
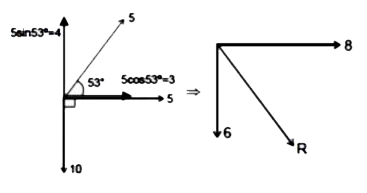
Resultant Amplitude
|R|=√82+62=10
|
Topper's Solved these Questions
- NTA TPC JEE MAIN TEST 100BOOK - NTA MOCK TESTSCHAPTER - NTA TPC JEE MAIN TEST 100EXERCISE - PHYSICS (SUBJECTIVE NUMERICAL)
10 Videos
- NTA NEET TEST 98BOOK - NTA MOCK TESTSCHAPTER - NTA NEET TEST 98EXERCISE - PHYSICS
45 Videos
- NTA TPC JEE MAIN TEST 101BOOK - NTA MOCK TESTSCHAPTER - NTA TPC JEE MAIN TEST 101EXERCISE - PHYSICS
30 Videos
Similar Questions
Knowledge Check
Find the resultant amplitude of the following simple harmonic equations :
x1=5sinωt
x2=5sin(ωt+53∘)
x3=−10cosωtA5B10C15D20The resultant amplitude due to superposition of three simple harmonic motions x1=3sinωt,
x2=5sin(ωt+37∘) and x3=−15cosωt isA18B10C12DNone of theseThe resultant amplitude due to super position of x1=sinωt,x2=5sin(ωt+37∘) and x3=−15cosωt is :
A17B21C13DNone of these
Find the displacement equation of the simple harmonic motion obtained by combining the motion.
x1=2sinωt, x2=4sin(ωt+π6) and x3=6sin(ωt+π3)
View SolutionFind the amplitude of the harmonic motion obtained by combining the motions
x1=(2.0cm)sinωt
and x2=(2.0cm)sin(ωt+π/3).
View SolutionIf i1=3sinωtand(i2)=4cosωt, then (i3) is

View SolutionThe ratio of amplitudes of following SHM is x1=Asinωtandx2=Asinωt+Acosωt
View SolutionChoose the most appropriate option.
What will be the displacement equation, of the simple harmonic motion obtained by combining the motions?
x1=2sinωt,x2=4sin(ωt+π6)
x3=6sin(ωt+π3)
View Solution