In the given figure magnetic field at the centre of ring O is 8√2 T. Now it is turned through 90∘ about x x' axis, so that two semicircular parts are mutually perpendicular. What is the new value of the magnetic field (in tesla) at the centre?

The correct Answer is:04.00
Given, μ0i2R=8√2T
ln 2nd case,
∣∣→B∣∣=√(μ0i4R)2+(μ0i4R)2=μ0i2√2R=4T
Topper's Solved these Questions
- NTA TPC JEE MAIN TEST 108BOOK - NTA MOCK TESTSCHAPTER - NTA TPC JEE MAIN TEST 108EXERCISE - PHYSICS (SUBJECTIVE NUMERICAL)
10 Videos
- NTA TPC JEE MAIN TEST 107BOOK - NTA MOCK TESTSCHAPTER - NTA TPC JEE MAIN TEST 107EXERCISE - PHYSICS
30 Videos
- NTA TPC JEE MAIN TEST 109BOOK - NTA MOCK TESTSCHAPTER - NTA TPC JEE MAIN TEST 109EXERCISE - PHYSICS
30 Videos
Similar Questions
In the given figure magnetic field at the center of ring (O) is 8√2T . Now it is turned through a 90∘ about xx axis,so that two semicircular parts are mutually perpendicular.Find the value of magnetic field (in tesla) at centre
View SolutionA current l flows through a closed loop as shown in figure .The magnetic field at the centre O is
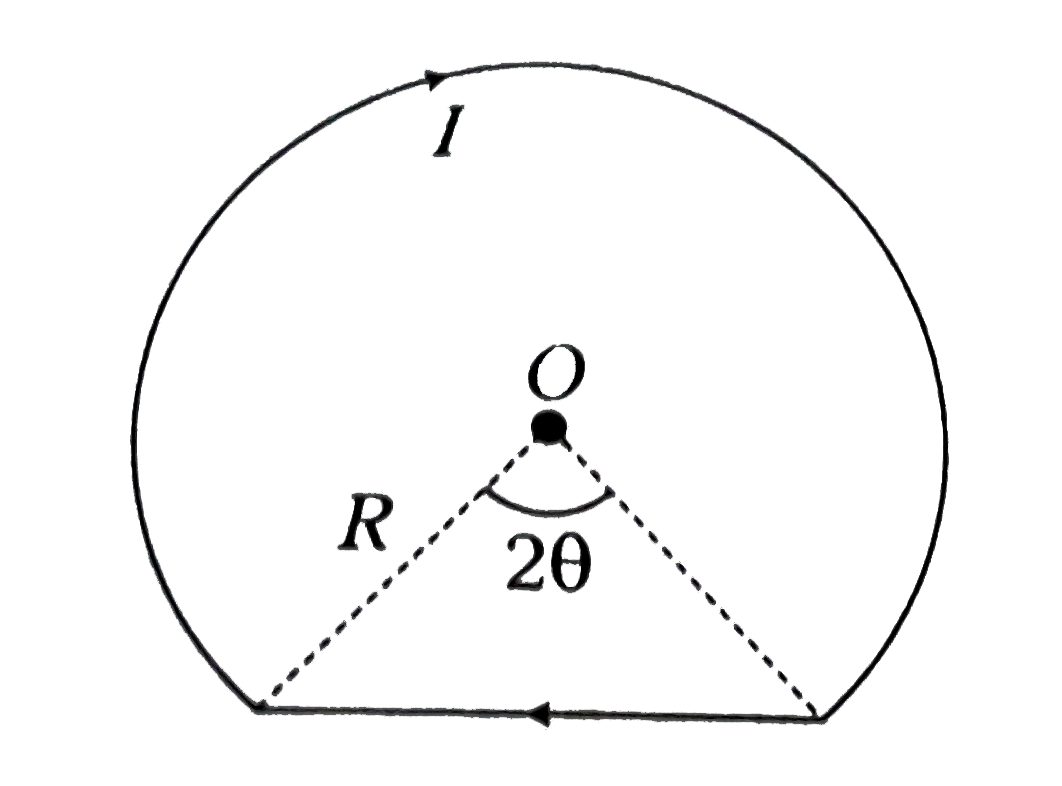
View Solution
Knowledge Check
A current I flows through a closed loop as shown in figure .The magnetic field at the centre O is
 Aμ0I2πR(π−θ+tanθ)Bμ0I2πR(π−θ+sinθ)Cμ0I2πR(θ+sinθ)DNone of these
Aμ0I2πR(π−θ+tanθ)Bμ0I2πR(π−θ+sinθ)Cμ0I2πR(θ+sinθ)DNone of theseAt what distance on the axis, from the centre for circular current carrying coil of radius r, the magnetic field becomes 1/8 th of the magnetic field at centre?
A√2rB23/2rC√3rD3√2rA current I, flowing in a long and straight wire along z-axis, is directed into two identical semicircular portions lying in y-z and x-z planes as shown in the figure. The magnetic field at the centre O is
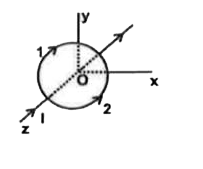 AzeroBμ0l4πCμ0l2√2rDμ0l√2r
AzeroBμ0l4πCμ0l2√2rDμ0l√2r
If the outer coil of the precious problem is rotated through 90^@ about a diameter, what would be the magnitude of the magnetic field B at the centre ?
View SolutionA square loop of side length L carries a current which produces a magnetic field B0 at the centre (O) of the loop. Now the square loop is folded into two parts with one half being perpendicular to the other (see fig). Calculate the magnitude of magnetic field at the centre O.

View SolutionAs current I flowing through the loop as shown in figure. The magnetic field at the centre O is
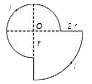
View SolutionA current I, flowing in a long and straight wire along z-axis, is directed into two identical semicircular portions lying in y-z and x-z planes as shown in the figure. The magnetic field at the centre O is

View SolutionA current carrying wire AB of the length L is turned along a circle, as shown in figure. The magnetic field at the centre O.

View Solution
