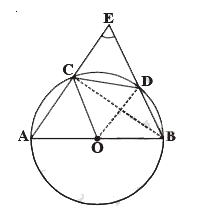
In figure, ¯¯¯¯¯¯AB is a diameter of the circle, ¯¯¯¯¯¯CD is a chord equal to the radius of the circle. ¯¯¯¯¯¯AC and ¯¯¯¯¯¯BD when extended intersect at a point E. Prove that ∠AEB=6∘.
 Solution in Telugu
Solution in Telugu
The correct Answer is:∠AEB=60∘
Step by step video & image solution for In figure, bar(AB) is a diameter of the circle, bar(CD) is a chord equal to the radius of the circle. bar(AC) and bar(BD) when extended intersect at a point E. Prove that angle AEB = 6^@. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLESBOOK - NCERT TELUGUCHAPTER - CIRCLESEXERCISE - DO THIS
6 Videos
- CIRCLESBOOK - NCERT TELUGUCHAPTER - CIRCLESEXERCISE - TRY THIS
9 Videos
- AREAS BOOK - NCERT TELUGUCHAPTER - AREAS EXERCISE - EXERCISE 11.3
10 Videos
- CO-0RDINATE GEOMETRYBOOK - NCERT TELUGUCHAPTER - CO-0RDINATE GEOMETRYEXERCISE - EXERCISE
99 Videos
Similar Questions
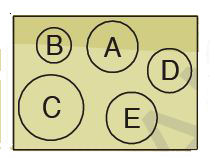
In the figure, which circles are congruent to the circle A?
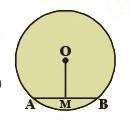
View SolutionIn a circle with centre 'O' . ¯¯¯¯¯¯AB is a chord and 'M' is its midpoint . Now prove that ∠(OM) is perpendicular to AB
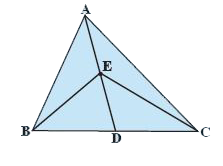
View SolutionIn a triangle ABC (see figure), E is the midpoint of median AD, show that
(i) ar ΔABE=arΔACE
(ii) arΔABE=14ar(ΔABC)
View SolutionThe set of intelligent students in a class is
View SolutionIn the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.

View SolutionIn the figure given below, bar(ED)||bar(AB) and bar(EF)||bar(BC) . If /_FED =40^(@) and /_ DEC =20^(@) , then the angle made by bar(BC) at the centre is
View SolutionIn the figure below, ¯¯¯¯¯¯AB∣∣∣∣¯¯¯¯¯¯FC,¯¯¯¯¯¯AE∣∣∣∣¯¯¯¯¯¯BC and ¯¯¯¯¯¯AF∣∣¯¯¯¯¯¯BD. If ∠F=x∘,∠C=γ∘,∠EAB=k∘ and ∠ABD=p∘, then which of the following options is correct ?
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_VIII_C16_E05_004_Q01.png" width="80%"gt
View Solution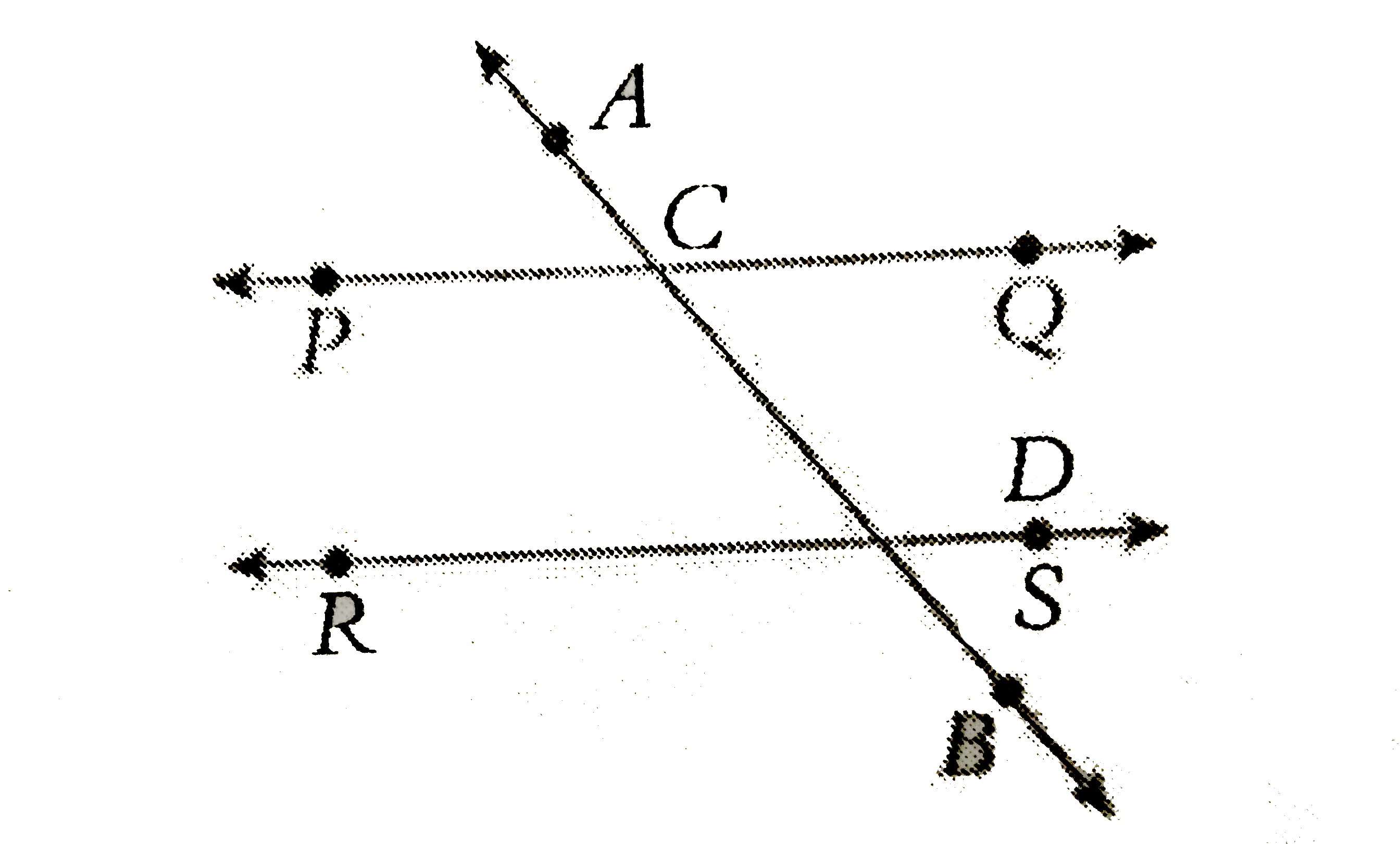
In the figure above, ¯¯¯¯¯¯PQand¯¯¯¯¯RS are parallel. ¯¯¯¯¯¯AC is transversal of ¯¯¯¯¯¯PQand¯¯¯¯¯RS. If ∠(ACP)=5x−70∘and∠BDR=4x+70∘, then find the value of x.
View SolutionIn the following figure, if O is the center of the circle and ¯¯¯¯¯¯AB is the diameter, then find ∠ACB.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E02_009_Q01.png" width="80%"gt
View SolutionIn the following figure, ¯¯¯¯¯¯BD is produced to E. If ¯¯¯¯¯¯AD is the angle bisector of ∠A, then find the ∠BCD.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E03_005_Q01.png" width="80%"gt
View SolutionIn the following figure, ¯¯¯¯¯¯DE and ¯¯¯¯¯¯FG are equal chords of the circle subtending ∠DHE and ∠FHG at the point H on the circle. If ∠DHE=23(12)2, then find ∠FHG.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E04_008_Q01.png" width="80%"gt
View SolutionIn the given figure, ¯¯¯¯¯¯AD and ¯¯¯¯¯¯BE intersect at C, such that BC = CE, ∠ABC=40∘ and ∠DEC=85∘. Find ∠BAC−∠CDE.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E04_027_Q01.png" width="80%"gt
View SolutionIn the given figure, PQRS is a parallelogram. A and B are the mid-point of ¯¯¯¯¯¯PQ and ¯¯¯¯¯SR respectively. If PS=BR, then the quadrilateral ADBC is a…………………… ,
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E05_020_Q01.png" width="80%"gt
View SolutionIn the figure given below (not to scale), D is a point on the circle with center A and C is a point on the circle with centers B, ¯¯¯¯¯¯AD⊥¯¯¯¯¯¯BD and ¯¯¯¯¯¯BC⊥¯¯¯¯¯¯CA. Then which of the following is true?
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E06_004_Q01.png" width="80%"gt
View SolutionIn the figure (not to scale) AB = AC and BD = CD. Find ∠ADB
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C15_E05_003_Q01.png" width="80%"gt
View SolutionThe resultant of the three vectors ¯¯¯¯¯¯OA,¯¯¯¯¯¯OB and ¯¯¯¯¯¯OC shown in figure :-
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R01_E02_023_Q01.png" width="80%"gt
View Solution
