A particle travels along a semicircle of radius R in 2 s. The velocity of the particle is
πR
R
2πR
2R
The correct Answer is:B
Velocity =DisplacementTime taken=2R2=R
Similar Questions
The acceleration time graph of the motion of a particle from A to B is semicircle with radius of √7 . Find the velocity of particle at t2 at it t1 velocity is 3m/sec[π=22/7] .
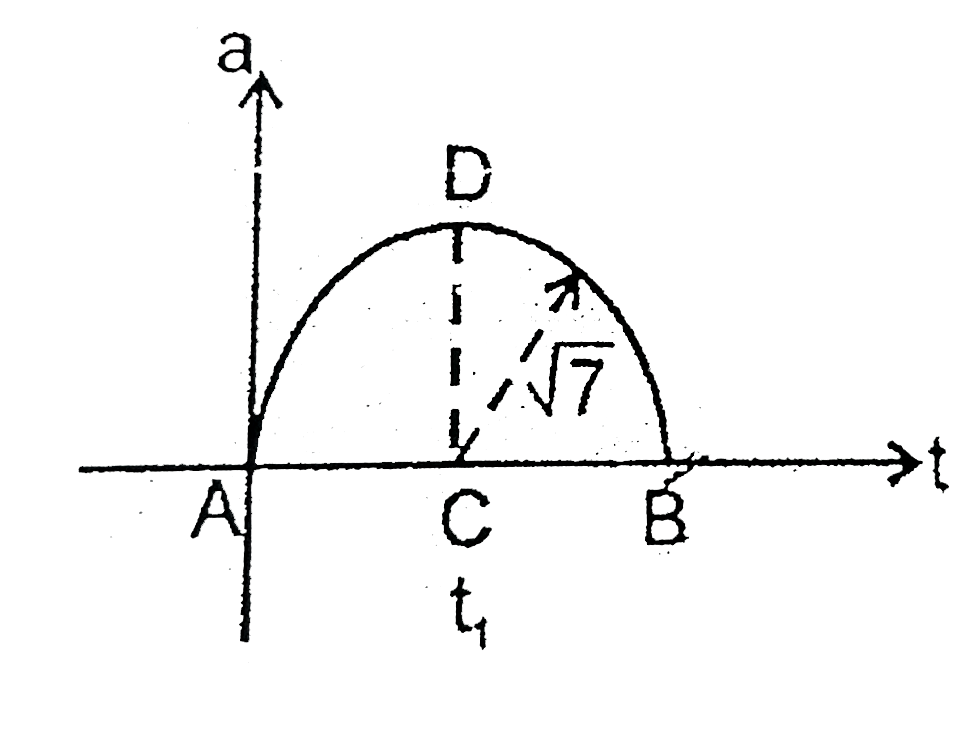
View SolutionA particle travels along the arc of a circle of radius r. Its speed depends on the distance travelled l as v=a√l where 'a' is a constant. The angle α between the vectors of net acceleration and the velocity of the particle is
View Solution
Knowledge Check
A particle moves along a semicircle of radius 10m in 5 seconds. The average velocity of the particle is
A2πms−1B4πms−1C2ms−1D4ms−1In 1 s, a particle goes from poitn A to point B, moving in a semicircle of radius 1 m. The magnitude of the average velocity of the particle is
A3.14m/sB2m/sC1m/sDzeroA particle is moving with uniform speed 0.5m/s along a circle of radius 1m then the angular velocity of particle is (in rads−1)
A2B1.5C1D0.5
A particle of mass M is revolving along a circule of radius R and nother particle of mass m is recolving in a circle of radius r. If time periods of both particles are same, then the ratio of their angular velocities is
View SolutionThe acceleration time graph of the motion of a particle from A to B is semicircle with radius of √7 . Find the velocity of particle at t2 at it t1 velocity is 3m/sec[π=22/7] .
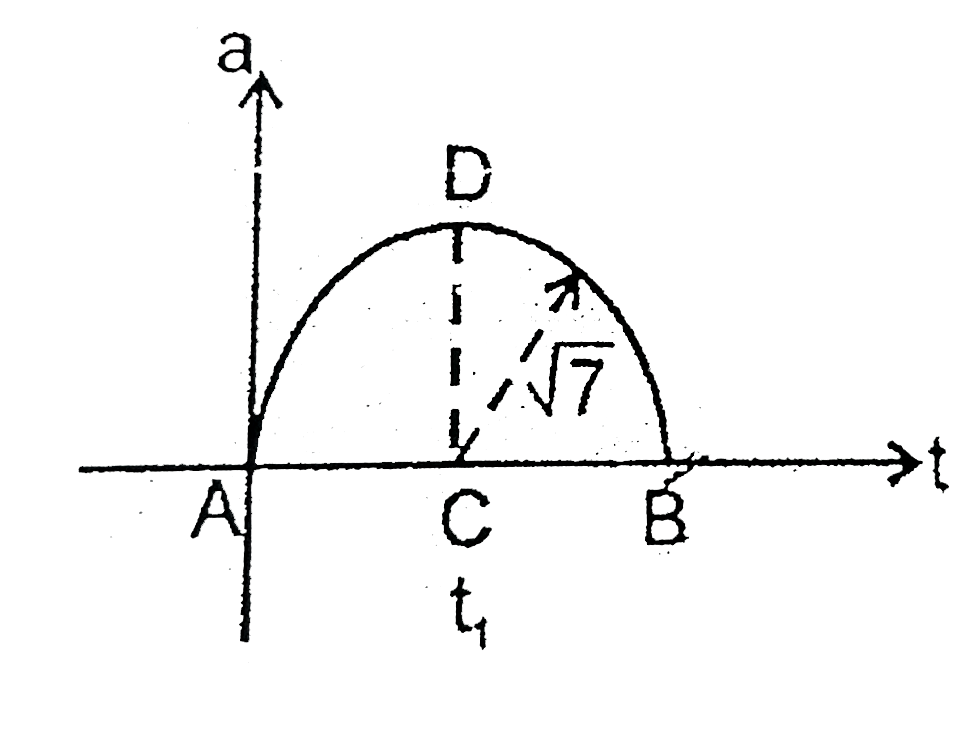
View SolutionA particle travels along the arc of a circle of radius r. Its speed depends on the distance travelled l as v=a√l where 'a' is a constant. The angle α between the vectors of net acceleration and the velocity of the particle is
View SolutionA particle moves along a circle of radius R =1m so that its radius vector →r relative to a point on its circumference rotates with the constant angular velocity ω=2rad/s. The linear speed of the particle is
View SolutionA particle of mass M is revolving along a circule of radius R and nother particle of mass m is recolving in a circle of radius r. If time periods of both particles are same, then the ratio of their angular velocities is
View Solution
