State the AA criterion of similarity of triangles.
Step-by-Step Text Solution:
1. Understanding the AA Criterion: The AA (Angle-Angle) criterion states that if two triangles have two angles of one triangle equal to two angles of another triangle, then the two triangles are similar.
2. Defining Similar Triangles: Two triangles are said to be similar if their corresponding angles are equal and their corresponding sides are in proportion.
3. Stating the AA Criterion: The AA criterion can be formally stated as follows:
- If in two triangles, the angles of one triangle are respectively equal to the angles of the other triangle, then the two triangles are similar.
4. Conclusion: Therefore, if triangle ABC has angles ∠A, ∠B, and ∠C, and triangle DEF has angles ∠D, ∠E, and ∠F, and if ∠A = ∠D and ∠B = ∠E, then triangle ABC is similar to triangle DEF (denoted as ΔABC ~ ΔDEF).
---
- If in two triangles, the angles of one triangle are respectively equal to the angles of the other triangle, then the two triangles are similar.
Topper's Solved these Questions
- SAMPLE PAPER 5 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5 EXERCISE - Part - A (Section - II)
20 Videos
- SAMPLE PAPER 5 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5 EXERCISE - Part B (Section - III)
8 Videos
- SAMPLE PAPER 12 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 12 EXERCISE - PART - B (SECTION -V)
4 Videos
- SAMPLE PAPER (SELF ASSESSMENT) 12BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER (SELF ASSESSMENT) 12EXERCISE - PART-B (Section-V)
4 Videos
Similar Questions
State the ASA criterion of similarity of triangles.
View SolutionSimilarity of Two Triangles
View SolutionState ASA criterion of congruence of triangles.
View SolutionSimilar Triangles |Criteria For Similarity Of Triangles|NCERT Questions
View SolutionIf the ratio of the perimeter of two similar triangles is 4:25, then find the ratio of the areas of the similar triangles.
View SolutionIn the figure ∠ABC=75∘
∠EDC=75∘
State which two triangles are similar and by which test? Also
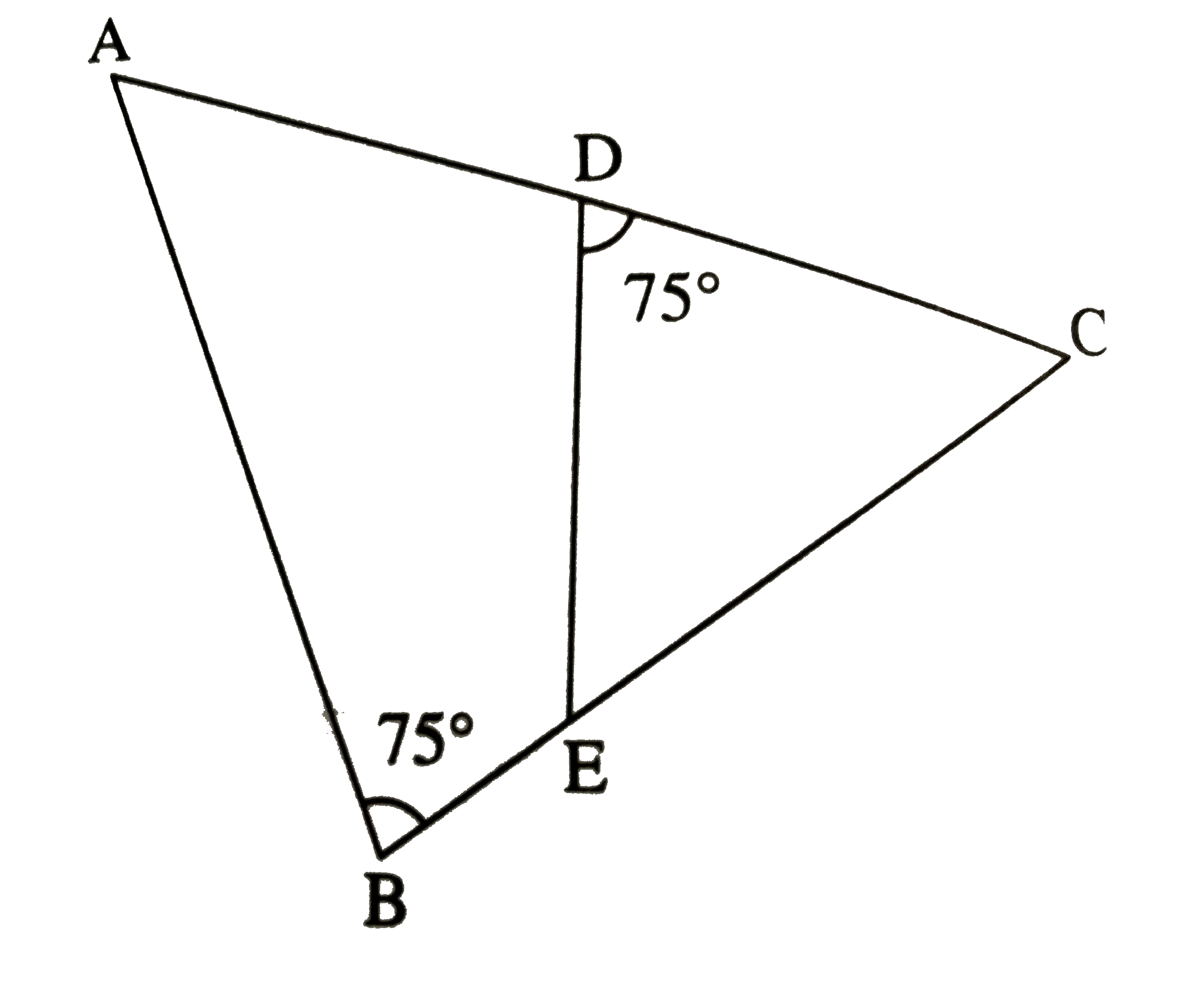
write the similarity of these two triangles by a proper one to one correspondence.
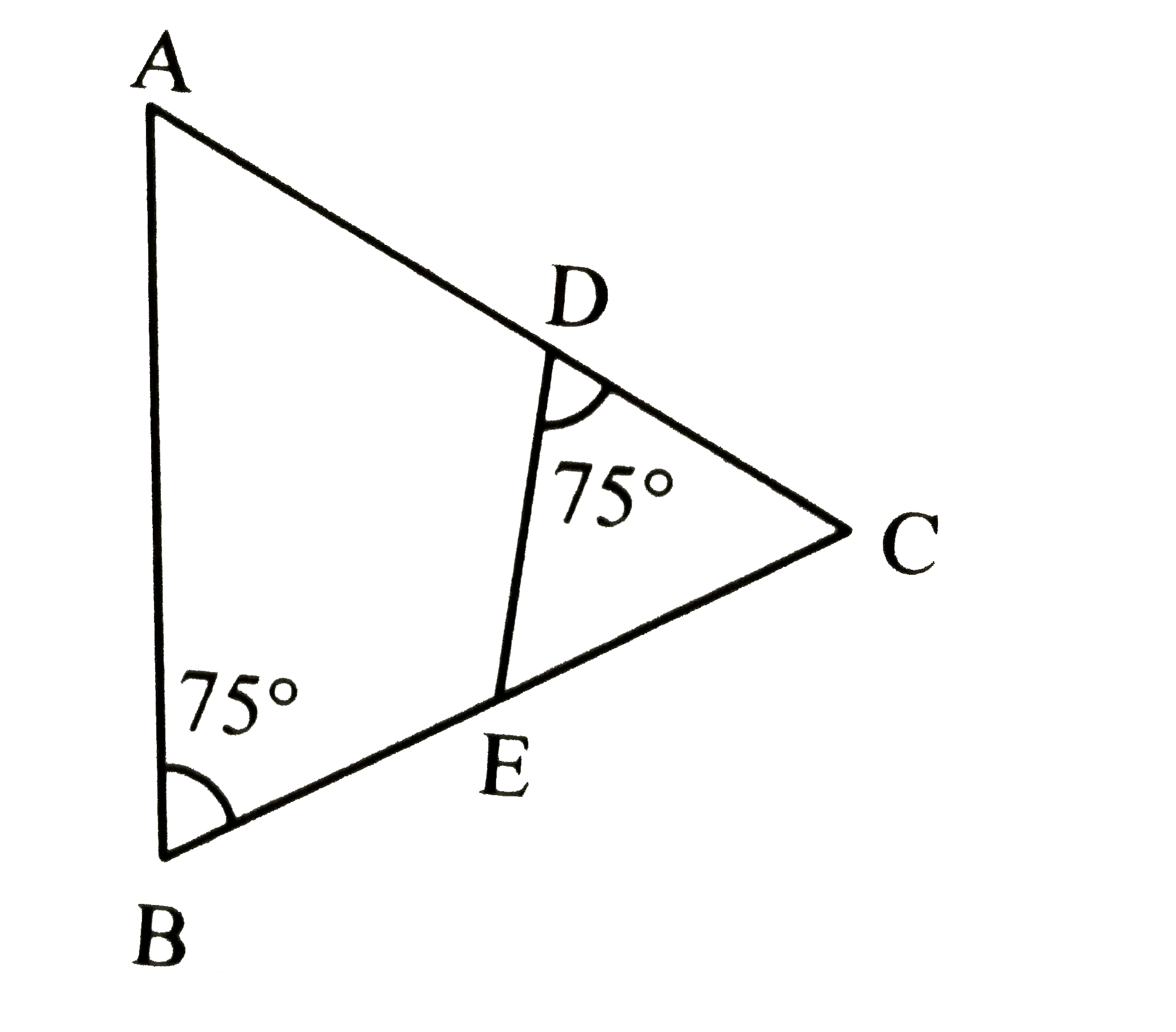
View SolutionIn the adjoining figure, ∠ABC=75∘,∠EDC=75∘. State which two triangle are similar and by which test? Also write the similarity of these two triangles by a proper one to one correspondence.
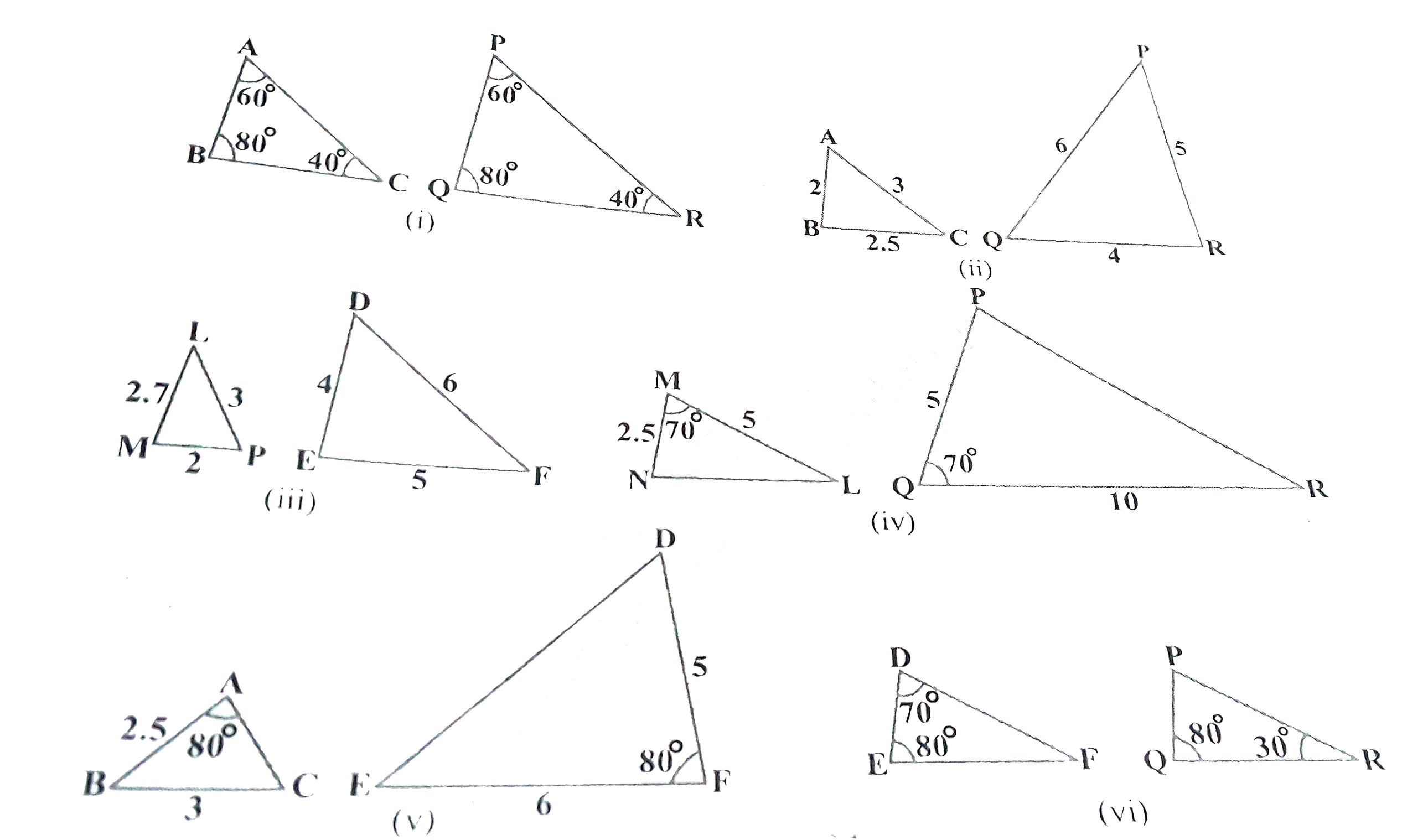
View SolutionState which pairs of triangles in Figure are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:
View SolutionState the pairs of triangles in the given figures are similar . Write the similarity criterion used by you for answering the question and also writer the pairs of similar triangles in the symbolic from :
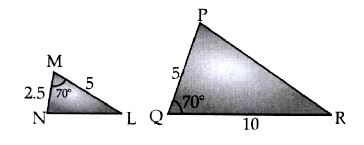
View SolutionState the pairs of triangles in the given figures are similar . Write the similarity criterion used by you for answering the question and also writer the pairs of similar triangles in the symbolic from :
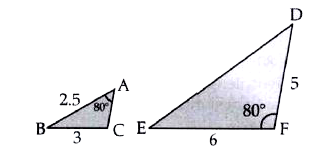
View Solution
