If in ΔABC,∠B=90∘,AB=6√3 and AC = 12, find BC.
The correct Answer is:6 cm
To solve the problem, we will use the Pythagorean theorem, which is applicable in right-angled triangles. In triangle ABC, angle B is 90 degrees, AB is given as 6√3, and AC is given as 12. We need to find the length of side BC.
1. Identify the sides of the triangle:
- Let AB=6√3 (one leg)
- Let BC=x (the other leg)
- Let AC=12 (the hypotenuse)
2. Apply the Pythagorean theorem:
The Pythagorean theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Therefore, we can write:
AC2=AB2+BC2
Substituting the known values:
122=(6√3)2+x2
3. Calculate the squares:
- Calculate 122:
122=144
- Calculate (6√3)2:
(6√3)2=62⋅(√3)2=36⋅3=108
4. Set up the equation:
Now we can substitute these values back into the equation:
144=108+x2
5. Isolate x2:
To find x2, we rearrange the equation:
x2=144−108
x2=36
6. Solve for x:
Taking the square root of both sides gives:
x=√36=6
7. Conclusion:
Therefore, the length of side BC is 6 units.
Final Answer:
BC = 6 units.
- Let AB=6√3 (one leg)
- Let BC=x (the other leg)
- Let AC=12 (the hypotenuse)
The Pythagorean theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Therefore, we can write:
AC2=AB2+BC2
Substituting the known values:
122=(6√3)2+x2
- Calculate 122:
122=144
- Calculate (6√3)2:
(6√3)2=62⋅(√3)2=36⋅3=108
Now we can substitute these values back into the equation:
144=108+x2
To find x2, we rearrange the equation:
x2=144−108
x2=36
Taking the square root of both sides gives:
x=√36=6
Therefore, the length of side BC is 6 units.
BC = 6 units.
Topper's Solved these Questions
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5 EXERCISE - Part - A (Section - II)20videos
SAMPLE PAPER 5
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5 EXERCISE - Part B (Section - III)8videos
SAMPLE PAPER 5
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 12 EXERCISE - PART - B (SECTION -V)4videos
SAMPLE PAPER 12
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER (SELF ASSESSMENT) 12EXERCISE - PART-B (Section-V)4videos
SAMPLE PAPER (SELF ASSESSMENT) 12
Similar Questions
Knowledge Check
- Question 1 - Select One
If in ΔABC,∠B=90∘,AB=6√3 and AC=12cm, find BC.
A5 cmB6 cmC7 cmD8 cm - Question 2 - Select One
In a ΔABC,∠B=90∘,∠C=45∘ and D is mid point of AC. If AC = 4√2 unit then BD is
A52 unitB2 unitC2√2 unitD4√2 unit - Question 3 - Select One
Find the area of ΔABC in which ∠B=90∘, BC = 8 cm and AC=10 cm. If BD⊥AC, then find BD.
A4. 8 cmB8. 4 cmC3.7 cmDnone of these
In ΔABC,
∠C=90∘,
∠B=60∘,
∠C=6. Find AB.View SolutionIn ΔABC,∠B=90∘ , AB = 8, BC = 6 and BD is a median . Find / (BD).
View SolutionSee the gven figure. In ΔABC,∠B=90∘,∠A=30∘,AC=14, then findAB and BC.
View SolutionIn ΔABC,∠B=90∘,∠A=30∘,b=20cm, find a and c.
View SolutionIn right ΔABC, ∠B=90∘, AB=3cm and AC=6cm. Find ∠A.
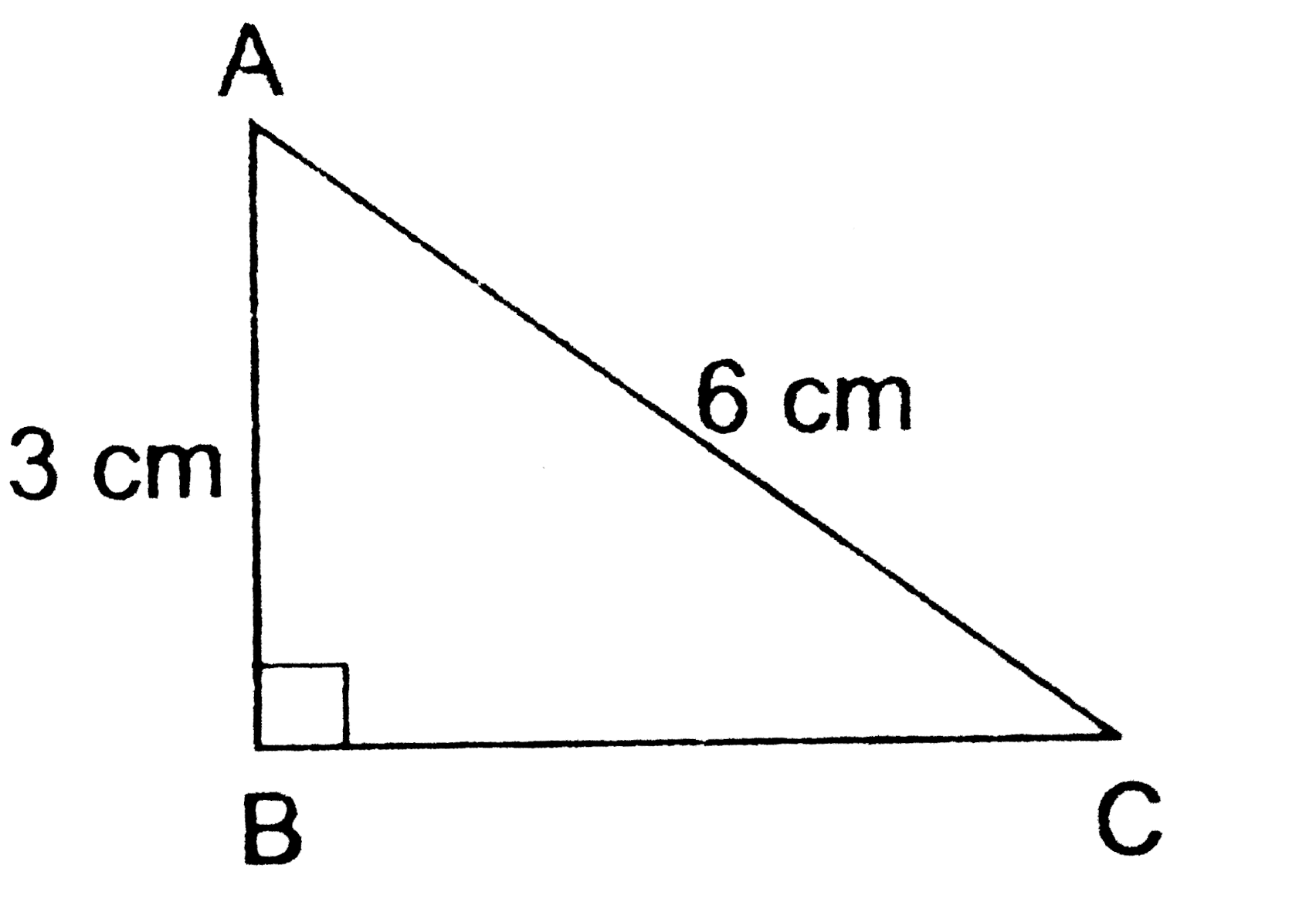 View Solution
View Solution

