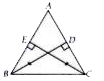
In ΔABC,∠A is acute. BD and CE are perpendicular on AC and AB respectively. Prove that AB×AE=AC×AD.
The correct Answer is:AC×AD
Step by step video, text & image solution for In DeltaABC, angleA is acute. BD and CE are perpendicular on AC and AB respectively. Prove that ABxxAE=ACxxAD. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SAMPLE PAPER 10 SOLVED BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 10 SOLVED EXERCISE - PART - B (SECTION - V)
4 Videos
- SAMPLE PAPER 10 SOLVED BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 10 SOLVED EXERCISE - PART - B (SECTION - III)
8 Videos
- SAMPLE PAPER 10 (SELF-ASSESSMENT)BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 10 (SELF-ASSESSMENT)EXERCISE - Section-C (Case Study Based Questions)
10 Videos
- SAMPLE PAPER 11BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 11EXERCISE - PART -B (SECTION-V)
4 Videos
Similar Questions
Knowledge Check
In ΔABC,BDandCEareperpendica––r→ACandABrespectively.IfBD = CE,thenDelta ABC is
AEquilateralBIsoscelesCRight-angledDScaleneIn the adjoining figure D is the midpoint of BC of a ΔABC,DMandDN are the perpendiculars on AB and AC respectively and DM=DN, then the ΔABC is :
 Aright angledBisoscelesCequilateralDscalene
Aright angledBisoscelesCequilateralDscaleneIf ΔABC,∠A=52∘, Its sides AB and AC are produced to the points D and E respectively. If the bisectors of the ∠CBDand∠BCE meet at point O, then ∠BOC is equal to:
A106∘B64∘C16∘D32∘
In a △ABC the angles at B and C are acute. If BE and CF be drawn perpendiculars on AC and AB respectivel, prove that
BC2=Ab×BF+AC×EC
View SolutionIn ΔABC,∠Band∠C are acute angles. BE and CF are perpendicular from vertices B and C on sides AC and AB respectively. Then BC2 is equal to-
View SolutionIn ΔABC,AB=AC and the bisectors of ∠B and ∠C meet AC and AB at point D and E respectively. Prove that BD=CE.
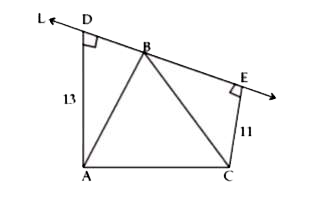
View SolutionThe figure shows an equilateral ΔABC with a line L passing through B. AD and CE are perpendicular to L respectively. If AD = 13 and CE = 11 find AC = ?
View SolutionIn a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=12(AB−CD).

View Solution