Five congruent circles of radius 1 cm each, intersect in such a way that the chord is of length 1 cm. Total area of all the dotted regions is :

4π12−√34cm2
π6−√34cm2
4π6−√34cm2
8π6−√34cm2
The correct Answer is:D
Step by step video & image solution for Five congruent circles of radius 1 cm each, intersect in such a way that the chord is of length 1 cm. Total area of all the dotted regions is : by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SAMPLE PAPER 1BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 1EXERCISE - Section -C
10 Videos
- SAMPLE PAPER 1BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 1EXERCISE - Section -A
20 Videos
- SAMPLE PAPER 07BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 07EXERCISE - SECTION -C
10 Videos
- SAMPLE PAPER 10BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 10EXERCISE - SECTION-C
10 Videos
Similar Questions
Given below is the picture of the Olympic rings made by taking five congruent circles of radius 1cm each, intersecting in such a way that the chord formed by joining the point of intersection of two circles is also of length 1cm. Total area of all the dotted regions assuming the thickness of the rings to be negligible is

View SolutionIn a circle of radius 13 cm, AB and CD are two equal and chords of lengths 24 cm each .What is the distance between the chords ?
View Solution
Knowledge Check
In a circle of radius 10 cm, with centre O, PQ and PR are two chords each of length 12 cm. PO intersects chord QR at the points S. The length of OS is :
त्रिज्या 10 सेमी तथा केंद्र O वाले एक वृत्त में, PQ तथा PR दो जीवाएं हैं जिनमें से प्रत्येक की लंबाई 12 सेमी है | PO, जीवा QR को बिंदु S पर काटती है |OS की लंबाई है :A2.8 cm.B2.5 cm.C3.2 cm.D3 cm.Two equal circles of radius 4 cm intersect each other such that each passes through the centre of the other. The length of the common chord is :
A2√3 cmB4√3 cmC2√2 cmD8 cmTwo identical circles each of radius 4 cm intersect such that the circumference of each one passes through the centre of the other. What is the area (in cm2) of the intersecting region?
A16π3−4√3B32π3−4√3C32π3−8√3D64π3−16√3
In a circle of radius 5 cm, AB and Ac are two chords of 6cm each. Find the length of the chord BC.
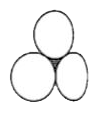
View SolutionThree circle of equal radii touch each other as shown in figure . The radius of each circle is 1 cm. What is the area of shaded region ?
View SolutionIn a circle of radius 10 cm, a chord is at a distance of 6 cm from the centre. The length of chord is
View SolutionTwo identical circles each of radius 2 cm intersect each other such that the circumference of each one passes through the centre of the other. What is the area (in cm2) of the intersecting region ?
View SolutionIn a circle of radius 17 cm a chord is at a distance of 15 cm form the centre of the circle. What is the length of the chord ?
View Solution
