What are the values of x and y in the system of linear equations 4x+5y=−3 and 2x−y=2 ?
(-3, -2)
(3, 2)
(-3, 2)
(3, -2)
The correct Answer is:D
To solve the system of linear equations given by:
1. 4x+5y=−3 (Equation 1)
2. 2x−y=2 (Equation 2)
we can use the method of elimination or substitution. Here, we'll use elimination.
Step 1: Make the coefficients of y the same
To eliminate y, we can multiply Equation 2 by 5 to match the coefficient of y in Equation 1.
5(2x−y)=5(2)
This gives us:
10x−5y=10(Equation 3)
Step 2: Rewrite the equations
Now we have:
1. 4x+5y=−3 (Equation 1)
2. 10x−5y=10 (Equation 3)
Step 3: Add the equations
Now, we can add Equation 1 and Equation 3 together to eliminate y:
(4x+5y)+(10x−5y)=−3+10
This simplifies to:
14x=7
Step 4: Solve for x
Now, divide both sides by 14:
x=714=12
Step 5: Substitute x back into one of the original equations
Now that we have x, we can substitute it back into Equation 2 to find y:
2x−y=2
Substituting x=12:
2(12)−y=2
This simplifies to:
1−y=2
Step 6: Solve for y
Now, isolate y:
−y=2−1
−y=1
y=−1
Final Values
Thus, the values of x and y are:
x=12,y=−1
Summary
The solution to the system of equations is:
- x=12
- y=−1
---
2. 2x−y=2 (Equation 2)
To eliminate y, we can multiply Equation 2 by 5 to match the coefficient of y in Equation 1.
Now we have:
2. 10x−5y=10 (Equation 3)
Now, we can add Equation 1 and Equation 3 together to eliminate y:
Now, divide both sides by 14:
Now that we have x, we can substitute it back into Equation 2 to find y:
Now, isolate y:
−y=1
y=−1
Thus, the values of x and y are:
The solution to the system of equations is:
- x=12
- y=−1
Topper's Solved these Questions
- SAMPLE PAPER 03BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 03EXERCISE - Section - B
20 Videos
- SAMPLE PAPER 02BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 02EXERCISE - SECTION - D
9 Videos
- SAMPLE PAPER 03 (MATHEMATICS)BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 03 (MATHEMATICS)EXERCISE - SECTION D
12 Videos
Similar Questions
Knowledge Check
Calculate the value of a, if x = a and y = b is the solution of the linear equations x - y = 2 and x + y = 4.
A1B3C2D0The system of linear equations 3x-y-2z=2,2y-z=-1and3x-5y=3 has
Aa unique solutionBan infinitely many solutionsCno solutionDNone of the aboveFor what values of k, does the system of linear equations x + y + z = 2, 2x + y - z = 3, 3x + 2y + kz = 4 have a unique solution ?
Ak = 0B−1<k<1C−2<k<2Dk≠0
Solve graphically the system of linear equations x+2y=3,4x+3y=2
View SolutionFind the values of x and y which satisfy the equations:
y+4x=9 and 3y+2x=5
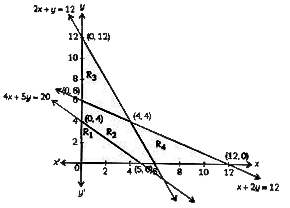
View SolutionWhich of the folowing should be the feasible region of the system of linear lnequalities x + 2y ≤12,2x+y≤12,4x+5y≥20 and x,y≥0 ?
View SolutionUse matrix method, solve the system of linear equations :
x+y=5, y+z=3, x+z=4.
View SolutionThe number of solutions of the pair of linear equations x + 3y = 4 and 2x + y = 5 is:
View Solution
