The graphical representation of x+2y−4=0and2x+4y−12=0 will be
coincident lines
parallel lines
intersecting lines
Data insufficient
To determine the graphical representation of the equations x+2y−4=0 and 2x+4y−12=0, we will analyze the coefficients of the equations and apply the conditions for consistency, parallelism, and intersection of lines.
1. Identify the coefficients:
For the first equation x+2y−4=0:
- a1=1
- b1=2
- c1=−4
For the second equation 2x+4y−12=0:
- a2=2
- b2=4
- c2=−12
2. Calculate the ratios:
We will calculate the ratios a1a2, b1b2, and c1c2.
- a1a2=12
- b1b2=24=12
- c1c2=−4−12=13
3. Analyze the conditions:
- For the lines to be consistent (intersecting), the condition a1a2=b1b2≠c1c2 must hold.
- For the lines to be parallel, the condition a1a2=b1b2 but c1c2≠c1c2 must hold.
- For the lines to be intersecting, the condition a1a2≠b1b2 must hold.
4. Evaluate the conditions:
- We have a1a2=12 and b1b2=12, which are equal.
- However, c1c2=13 is not equal to 12.
5. Conclusion:
Since a1a2=b1b2 and c1c2≠12, the lines represented by the equations are parallel.
Final Answer:
The graphical representation of the equations x+2y−4=0 and 2x+4y−12=0 will be parallel lines.
For the first equation x+2y−4=0:
- a1=1
- b1=2
- c1=−4
- a2=2
- b2=4
- c2=−12
We will calculate the ratios a1a2, b1b2, and c1c2.
- b1b2=24=12
- c1c2=−4−12=13
- For the lines to be consistent (intersecting), the condition a1a2=b1b2≠c1c2 must hold.
- For the lines to be parallel, the condition a1a2=b1b2 but c1c2≠c1c2 must hold.
- For the lines to be intersecting, the condition a1a2≠b1b2 must hold.
- We have a1a2=12 and b1b2=12, which are equal.
- However, c1c2=13 is not equal to 12.
Since a1a2=b1b2 and c1c2≠12, the lines represented by the equations are parallel.
The graphical representation of the equations x+2y−4=0 and 2x+4y−12=0 will be parallel lines.
Topper's Solved these Questions
- SAMPLE PAPER 10 (SELF-ASSESSMENT)BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 10 (SELF-ASSESSMENT)EXERCISE - Section-C (Case Study Based Questions)
10 Videos
- SAMPLE PAPER 10 (SELF-ASSESSMENT)BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 10 (SELF-ASSESSMENT)EXERCISE - Section-C (Case Study Based Questions)
10 Videos
- SAMPLE PAPER 10BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 10EXERCISE - SECTION-C
10 Videos
- SAMPLE PAPER 10 SOLVED BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 10 SOLVED EXERCISE - PART - B (SECTION - V)
4 Videos
Similar Questions
Knowledge Check
The graphical representation of the equations x+2y=3and2x+4y+7=0 gives a pair of
Aparallel linesBintersecting linesCcoincident linesDnone of theseThe graphical solution of the system of linear inequalities 3x,4y≥12,y≥1,x≥0 is
A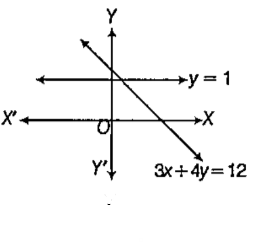 B
B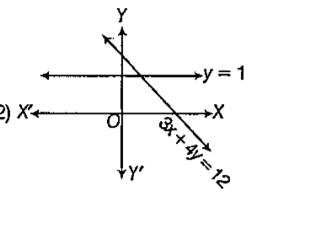 C
C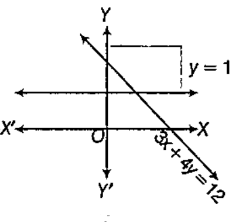 D
D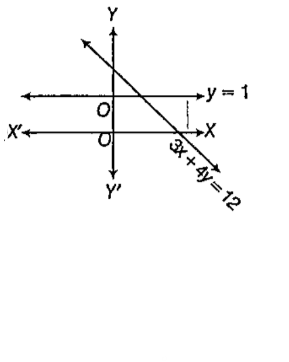
The circles x2+y2−2x−4y+1=0 and x2+y2+4y−1=0
Atouch internallyBtouch externallyChave 3x+4y−1=0 as the common tangent at the point of contact.Dhave 3x+4y+1=0 as the common tangent at the point of contact.
Find the parametric representation of circles :
(i) x2+y2+12x−4y−1=0
(ii) x2+y2+2gx+2fy+c=0.
View SolutionShow graphically that the system of equations
2x + 4y = 10 and 3x + 6y = 12 has no solution.
View SolutionStatement 1 : The equations of the straight lines joining the origin to the points of intersection of x2+y2−4x−2y=4 and x2+y2−2x−4y−4=0 is x−y=0 . Statement 2 : y+x=0 is the common chord of x2+y2−4x−2y=4 and x2+y2−2x−4y−4=0
View SolutionClassify the following pairs of lines as coincident, parallel, perpendicular or intersecting :
(i)6x+14y−16=0, 12x+28y−32=0
(ii)3x−4y=8, 3x+4y=11
(iii)5x−2y=7, 2y−5x=−7
(iv)4x+7y=19, 7x−4y=−2
(v)x−2y=7, 4y−2x=13
View SolutionThe path of a train A is given by the equation x+2y−4=0 and the path of another train B is given by the equation 2x+4y−12=0 . Represent this situation graphically.
View Solution
