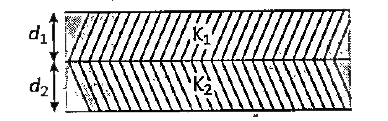
Two dielectric blocks in series make a parallel plate capacitor. Blocks are of thickness $d_{1}$ and $d_{2}$ respectively.

Effective dielectric constant is:

A

$\frac{K_{1} d_{1} + K_{2} d_{2}}{K_{1} + K_{2}}$

B

$\frac{K_{1} d_{1} + K_{2} d_{2}}{d_{1} + d_{2}}$

C

$\frac{2 K_{1} K_{2}}{K_{1} + K_{2}}$

D

$\frac{K_{1} K_{2} (d_{1} + d_{2})}{(K_{1} d_{2} + K_{2} d_{1})}$

Text Solution

Verified by Experts

The correct Answer is:D

Capacitance of Block 1.
$C_{1} = \frac{K_{1} ε_{0} A}{d_{1}}$
Capacitance of Block 2
$C_{2} = \frac{K_{2} ε_{0} A}{d_{2}}$
Since the two capacitors are in series
$\frac{1}{C} = \frac{1}{C_{1}} + \frac{1}{C_{2}}$
$C = \frac{C_{1} C_{2}}{C_{1} + C_{2}}$
$= \frac{K_{1} K_{2} ε_{0} A}{K_{1} d_{2} + K_{2} d_{1}}$
Equivalent capacitance is given by
$C = \frac{K ε_{0} A}{d_{1} + d_{2}}$
$K = \frac{K_{1} K_{2} (d_{1} + d_{2})}{K_{1} d_{2} + K_{2} d_{1}}$

|

Updated on:21/07/2023

Class 12 PHYSICS SAMPLE PAPER 04 (SOLVED)

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A parallel plate capacitor is made of two dielectric blocks in series. One of the blocks has thickness $d_{1}$ and dielectric constant $K_{1}$ and the other has thickness $d_{2}$ and dielectric constant $K_{2}$ as shown in figure. This arrangement can be through as a dielectric slab of thickness $d (= d_{1} + d_{2})$ and effective dielectric constant $K$ . The $K$ is.
.
A $\frac{K_{1} d_{1} + K_{2} d_{2}}{d_{1} + d_{2}}$
B $\frac{K_{1} d_{1} + K_{2} d_{2}}{K_{1} + K_{2}}$
C $\frac{K_{1} K_{2} (d_{1} + d_{2})}{K_{2} d_{1} + K_{1} d_{2}}$
D $\frac{2 K_{1} K_{2}}{K_{1} + K_{2}}$
Question 2 - Select One
A battery charges a parallel plate capacitor of thickness $(d)$ so that an energy $[U_{0}]$ is stored in the system. A slab of dielectric constant $(K)$ and thickness $(d)$ is then introduced between the plates of the capacitor. The new energy of the system is given by
A $K U_{0}$
B $K^{2} U_{0}$
C $\frac{U_{0}}{K}$
D $U_{0} / K^{2}$
Question 3 - Select One
The separation between the plates of a parallel plate capacitor is d and the area of each plate is A. iff a dielectric slab of thickness x and dielectric constant K is introduced between the plates, then the capacitance will be
A $\frac{ε_{0} A}{d - x (1 - \frac{1}{K})}$
B $\frac{ε_{0} A}{d + x (1 - \frac{1}{K})}$
C $\frac{ε_{0} A}{d + x (1 + \frac{1}{K})}$
D $\frac{ε_{0} A}{d - x (1 + \frac{2}{K})}$

EDUCART PUBLICATION-SAMPLE PAPER 04 (SOLVED)-SECTION-B

Home
Ask Doubt
Profile