In a uniform magnetic field of 5T, an electron is moving with constant velocity of 15m/s. The force on the electron is
75N
2.4×10−18N
1
zero
The correct Answer is:D
To find the force on an electron moving in a magnetic field, we can use the formula for the magnetic force:
F=q⋅(v×B)
where:
- F is the magnetic force,
- q is the charge of the electron,
- v is the velocity of the electron,
- B is the magnetic field strength,
- × denotes the cross product.
Step 1: Identify the values
- The charge of an electron, q=−1.6×10−19 C (the negative sign indicates the charge is negative).
- The velocity of the electron, v=15 m/s.
- The magnetic field strength, B=5 T.
Step 2: Calculate the magnitude of the force
Since the force is given by the cross product, we can simplify the calculation by considering the magnitude of the force:
F=|q|⋅v⋅B⋅sin(θ)
where θ is the angle between the velocity vector and the magnetic field vector. If we assume that the electron is moving perpendicular to the magnetic field (which gives the maximum force), then sin(θ)=1.
Thus, the formula simplifies to:
F=|q|⋅v⋅B
Step 3: Substitute the values into the equation
Now, substituting the known values into the equation:
F=(1.6×10−19C)⋅(15m/s)⋅(5T)
Step 4: Perform the calculation
Calculating the force:
F=1.6×10−19⋅15⋅5
Calculating 15⋅5=75:
F=1.6×10−19⋅75
Now, calculating 1.6⋅75=120:
F=120×10−19N
This can be expressed in scientific notation:
F=1.2×10−17N
Final Answer
The force on the electron is 1.2×10−17N.
---
- F is the magnetic force,
- q is the charge of the electron,
- v is the velocity of the electron,
- B is the magnetic field strength,
- × denotes the cross product.
- The charge of an electron, q=−1.6×10−19 C (the negative sign indicates the charge is negative).
- The velocity of the electron, v=15 m/s.
- The magnetic field strength, B=5 T.
Since the force is given by the cross product, we can simplify the calculation by considering the magnitude of the force:
Now, substituting the known values into the equation:
Calculating the force:
The force on the electron is 1.2×10−17N.
Topper's Solved these Questions
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - Section-B24videos
SAMPLE PAPER 6
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - Section-C6videos
SAMPLE PAPER 6
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - SECTION - C6videos
SAMPLE PAPER 5
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - SECTION-C6videos
SAMPLE PAPER 7
Similar Questions
An electron is moving northwards with a velocity 3⋅0×107ms−1 in a uniform magnetic field of 10T directed eastwards. Find the magnitude and direction of the magnetic force on the electron. (e=1⋅6×10−19C)
View SolutionAn electron emmited by a heated cathode and accelerated through a potential difference of 2⋅0kV enters a region with a uniform magnetic field of 0⋅15T. Determine the trajectory of the electron if the field (a) is transverse to its initial velocity (b) makes an angle of 30∘ with the initial velocity.
View Solution
Knowledge Check
- Question 1 - Select One
A straight conductor of length 1.5m moves in a uniform magnetic field of induction 5×10−3T with a velocity of 5m/s in a direction perpendicular to its length and also perpendicular to the field. The e.m.f. induced between the ends of the conductor is
A1.5×10−3VB3.75×10−3VC37.5×10−3VD25×10−3V - Question 2 - Select One
A long, narrow beam of electrons, of uniform cross-section consists of electrons moving with velcity v (c= velocity of light ). The ratio of the electric field to the magnetic field at any point near the beam is
AvBcCc2/vDv2/v - Question 3 - Select One
If an electron is moving with velocity v produces a magnetic field →B, then
Athe direction of field →B will be same as the direction of velocity →v.Bthe direction of field →B will be opposite to the direction of velocity →v.Cthe direction of field →B will be perpendicular to the direction of velocity →v.Dthe direction of field →B does not depend upon the direction of velocity →v.
The figure shows three situations when an electron moves with velocity →v travels through a uniform magnetic field →B. In each case, what is the direction of magnetic force on the electron
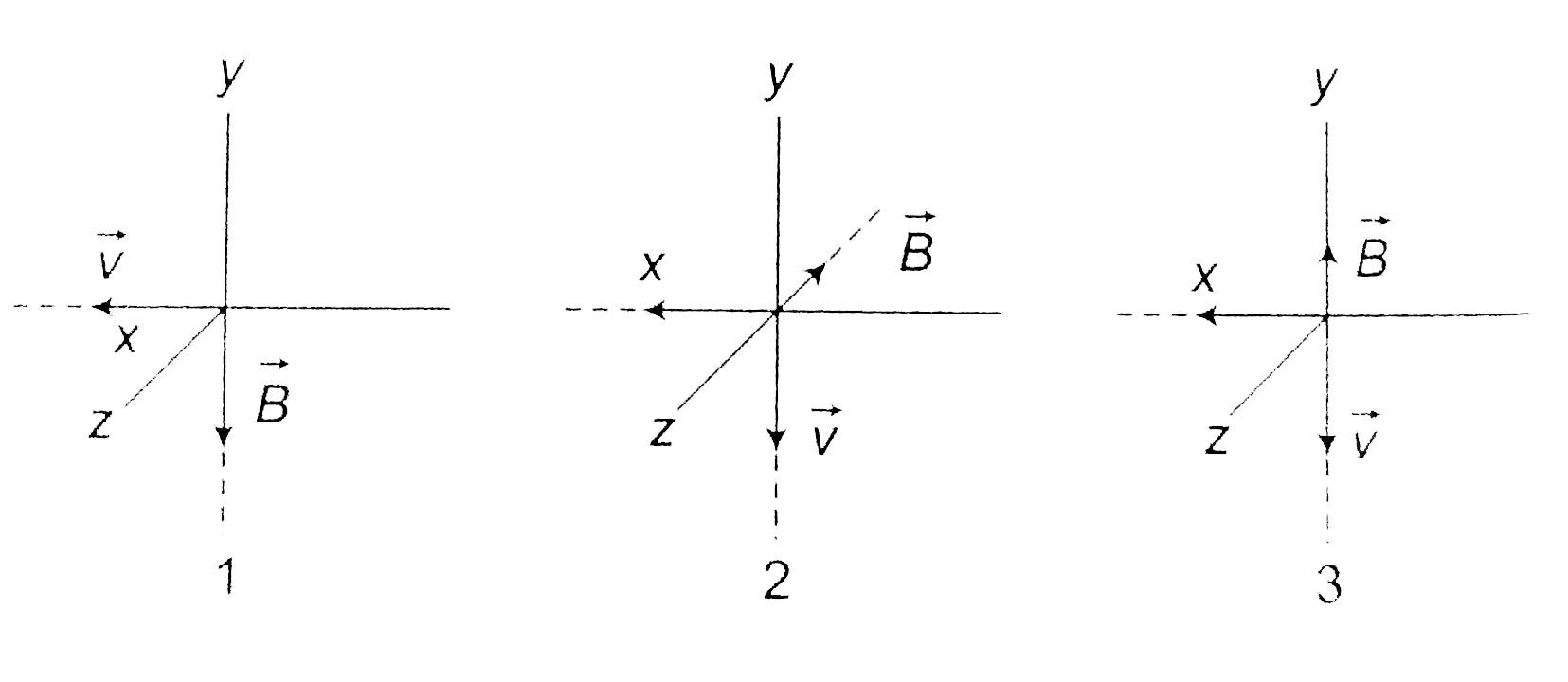 View Solution
View SolutionAn electron having momentum 2.4×10−23 kg m s−1 enters a region of uniform magnetic field of 0.15 T. The field vector makes an angle of 30∘ with the initial velocity vector of the electron. The radius of the helical path of the electron in the field shall be
View SolutionAn electron having momentum 2.4×10−23 kg m"/"s enters a region of unifom magnetic field of 0.15 T. The field vector makes an angle of 30∘ with the initial velocity Vector of the electron. The radius of the helical path of the electron in the field shall be
View SolutionA proton moving withh a velocity 2.5×107m/s enters a magnetic field of intensity 2.5T making an angle 30∘ with the magnetic field. The force on the proton is
View SolutionAn electron moving with a uniform velocity along the positive x-direction enters a magnetic field directed along the positive y-direction. The force on the electron is directed along
View Solution

