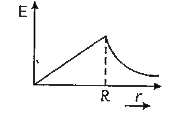
→E due to uniformly charged sphere of radius R as a function of distance from its centre is represented by

The correct Answer is:A
To find the electric field →E due to a uniformly charged sphere of radius R as a function of the distance r from its center, we need to consider two cases: when the point of interest is inside the sphere (i.e., r<R) and when it is outside the sphere (i.e., r≥R).
Step 1: Electric Field Inside the Sphere (r<R)
1. Gauss's Law: We apply Gauss's Law, which states that the electric flux through a closed surface is equal to the charge enclosed divided by the permittivity of free space (ϵ0).
ΦE=∮→E⋅d→A=Qencϵ0
2. Choose a Gaussian Surface: For a point inside the sphere, we choose a Gaussian surface that is a sphere of radius r (where r<R).
3. Charge Enclosed: The charge enclosed by this Gaussian surface can be found using the volume charge density ρ:
Qenc=ρ⋅V=ρ⋅43πr3
where ρ=Q43πR3 (the total charge Q is uniformly distributed over the volume of the sphere).
4. Substituting Charge into Gauss's Law:
ΦE=E⋅4πr2=ρ⋅43πr3ϵ0
E⋅4πr2=(Q43πR3)⋅43πr3ϵ0
5. Solving for E:
E=Q4πϵ0R3r
Thus, the electric field inside the uniformly charged sphere is:
→E=Q4πϵ0R3r^r
Step 2: Electric Field Outside the Sphere (r≥R)
1. Gauss's Law: Again, we apply Gauss's Law for a point outside the sphere.
2. Choose a Gaussian Surface: For r≥R, we choose a spherical Gaussian surface of radius r.
3. Charge Enclosed: The total charge Q of the sphere is enclosed by this Gaussian surface:
Qenc=Q
4. Substituting Charge into Gauss's Law:
ΦE=E⋅4πr2=Qϵ0
5. Solving for E:
E=Q4πϵ0r2
Thus, the electric field outside the uniformly charged sphere is:
→E=Q4πϵ0r2^r
Summary of Results
- For r<R:
→E=Q4πϵ0R3r^r
- For r≥R:
→E=Q4πϵ0r2^r
ΦE=∮→E⋅d→A=Qencϵ0
Qenc=ρ⋅V=ρ⋅43πr3
where ρ=Q43πR3 (the total charge Q is uniformly distributed over the volume of the sphere).
ΦE=E⋅4πr2=ρ⋅43πr3ϵ0
E⋅4πr2=(Q43πR3)⋅43πr3ϵ0
E=Q4πϵ0R3r
Thus, the electric field inside the uniformly charged sphere is:
→E=Q4πϵ0R3r^r
Qenc=Q
ΦE=E⋅4πr2=Qϵ0
E=Q4πϵ0r2
Thus, the electric field outside the uniformly charged sphere is:
→E=Q4πϵ0r2^r
→E=Q4πϵ0R3r^r
→E=Q4πϵ0r2^r
Topper's Solved these Questions
- SAMPLE PAPER 6BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - Section-B
24 Videos
- SAMPLE PAPER 6BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - Section-C
6 Videos
- SAMPLE PAPER 5BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - SECTION - C
6 Videos
- SAMPLE PAPER 7BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - SECTION-C
6 Videos
Similar Questions
If the potential at the center of a uniformly charged sphere of radius R is V then electric field at a distance r from the center of sphere will be (r<R) : -
View SolutionThe maximum electric field intensity on the axis of a uniformly charged ring of charge q and radius R is at a distance x from the centre of the ring.The value of x is
View Solution
Knowledge Check
The electric field due to uniformly charged sphere of radius R as a function of the distance from its centre is represented graphically by
A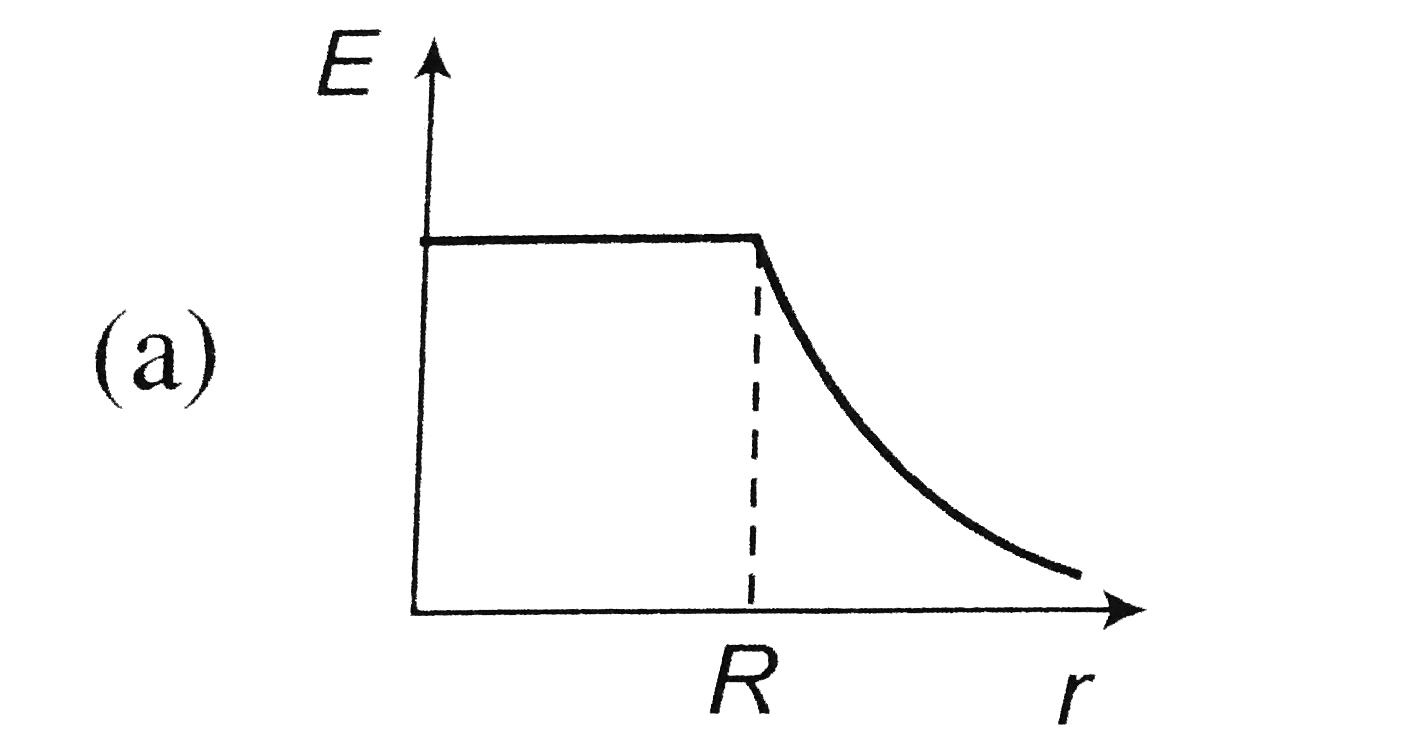 B
B C
C D
D
Graphical representation of electric field due to uniformly charged sphere of radius R as function of distance from its centre is given by:
A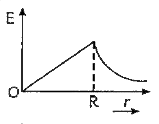 B
B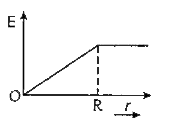 C
C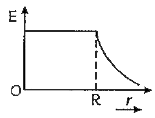 D
D
Which of the following graph represents the variation of electric field E due to a thin charged spherical shell of radius R as a function of the distance r from the centre of the shell?
A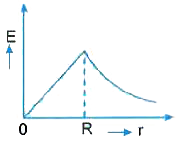 B
B CD
CD
If the potential at the centre of a uniformly charged hollow sphere of radus R is V, then electric field at a distance r from the centre of sphere will be (r>R).

View SolutionThe electric intensity due to a uniformly charged infinite cylinder of radius R , at a distance r(>R) , from its axis is proportional to
View SolutionA nonconducting sphere with radius a is concentric with and surrounded by a conducting spherical shell with inner radius b and outer radius c. The inner sphere has a negative charge uniformly distributed throughout its volume, while the spherical shell has no net charge. The potential V (r) as a function of distance from the center is given by

View SolutionThe electric field intensity at a distance 20cm from the centre of a uniformly charged non conducting solid sphere of radius 10cm is E.Then what is the electric field intensity at a distance 5cm from the centre it will be.....
View SolutionThe electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
View Solution
