In given triangle ABC ,OB and OC are bisectors of ∠Ba nd ∠C respectively then ∠BOC is equal to
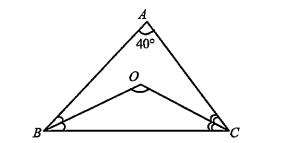
70∘
110∘
140∘
80∘
The correct Answer is:B
Similar Questions
In a △ABC, the bisectors of ∠B and ∠C meets at point O within the triangle. If ∠BOC is given, then which among the given option is true ?
△ABC में, ∠B तथा ∠C द्विभाजक त्रिभुज के भीतर बिंदु O पर मिलते हैं | यदि ∠BOC दिया गया है, तो निम्न में से कौन सा विकल्प सही होगा ?
View SolutionIn a △ABC, the bisectors of ∠B and ∠C meet at point O within the triangle. If ∠BOC is given, then which among the given options is true?
एक △ABC में, ∠B और ∠C के समदविभाजक, त्रिभुज के भीतर बिंदु O पर मिलते हैं| अगर ∠BOC दिया गया है तो निम्नलिखित विकल्पों में से कौन सा सही है?
View Solution
Knowledge Check
In a triangle ABC , OB and OC are the bisector of angle ∠B and ∠C respectively . ∠BAC=60∘ . The angle ∠BOC will be :
A150∘B120∘C100∘D90∘In a triangle, with usual notations, the length of the bisector of angle A is
A2bcb+csinA2B2bcb+ccosA2Cabc2R(b+c)cosecA2D4Ab+ccosecA2In figure, sides AB and AC of a ΔABC are produced to P and Q, respectively. The bisectors of ∠PBCand∠QCB intersect at O. Then, ∠BOC is equal to
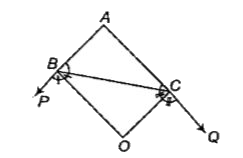 A90∘−12∠BACB12(∠PBC+∠QCB)C90∘+12∠BACDNone of the above
A90∘−12∠BACB12(∠PBC+∠QCB)C90∘+12∠BACDNone of the above
Triangle ABC is an isosceles triangle with AB=AC. Bisectors of ∠Band∠C intersect each other at O. join A−O and prove that
OB=OC
View SolutionIn a △ABC, the bisectors of ∠B and ∠C meets at point O inside the triangle. If ∠BOC=122∘, then the measure of ∠A
△ABCमें, ∠B तथा ∠C द्विभाजक त्रिभुज के भीतर बिंदु O पर मिलते हैं | यदि ∠BOC=122∘ है, तो ∠A का माप क्या होगा ?
View SolutionIn a △ABC, the bisectors of ∠B and ∠C meets at point O. If ∠BOC=142∘ then the measure∠A is:
△ABC में, ∠B तथा ∠C के द्विभाजक O पर मिलते हैं | यदि ∠BOC=142∘ है, तो ∠A का माप ज्ञात करे |
View SolutionIn given triangle ABC ,AP is bisector of ∠BAC and AQ is perpendicular to BC then ∠PAQ is equal to
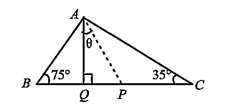
View SolutionIf in a ΔABC, O and O' are the incentre and orthocentre respectively, then (O'A+O'B+O'C) is equal to
View Solution
