A square and a circle have equal perimeters. The ratio of the area of the square to the area of the circle is
1:1
1:4
π:2
π:4
The correct Answer is:D
To solve the problem, we need to find the ratio of the area of a square to the area of a circle, given that they have equal perimeters.
1. Define Variables:
- Let the side of the square be A.
- Let the radius of the circle be R.
2. Write the Perimeter Formulas:
- The perimeter of the square is given by:
Psquare=4A
- The perimeter of the circle is given by:
Pcircle=2πR
3. Set the Perimeters Equal:
Since the perimeters are equal, we can write:
4A=2πR
4. Solve for A:
Rearranging the equation to solve for A:
A=2πR4=πR2
5. Calculate the Areas:
- The area of the square is:
Areasquare=A2=(πR2)2=π2R24
- The area of the circle is:
Areacircle=πR2
6. Find the Ratio of Areas:
Now, we can find the ratio of the area of the square to the area of the circle:
Ratio=AreasquareAreacircle=π2R24πR2
7. Simplify the Ratio:
Simplifying the ratio:
Ratio=π2R24⋅πR2=π4
Final Answer:
The ratio of the area of the square to the area of the circle is:
π4
- Let the side of the square be A.
- Let the radius of the circle be R.
- The perimeter of the square is given by:
Psquare=4A
- The perimeter of the circle is given by:
Pcircle=2πR
Since the perimeters are equal, we can write:
4A=2πR
Rearranging the equation to solve for A:
A=2πR4=πR2
- The area of the square is:
Areasquare=A2=(πR2)2=π2R24
- The area of the circle is:
Areacircle=πR2
Now, we can find the ratio of the area of the square to the area of the circle:
Ratio=AreasquareAreacircle=π2R24πR2
Simplifying the ratio:
Ratio=π2R24⋅πR2=π4
The ratio of the area of the square to the area of the circle is:
π4
Topper's Solved these Questions
Similar Questions
The perimeters of a reqular hexagon and a square are equal. The ratio of the area of the square to the area of the hexagon is:
View SolutionPQRS is a square. SR is a tangent (at point S) to the circle with centre O and TR = OS. Then, the ratio of area of the square to the area of the circle is :
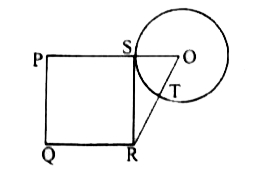
View Solution
Knowledge Check
The areas of a circle and a square are same. The ratio of the side of the square to the radius of the circle is
A2π:1B1:√πC√π:1D1:πA circle and a square have same area. The ratio of the side of the square to the radius of the circle will be :
A(a) √π:1B(b) 1:√πC(c) π2:1D(d) 1:πA circle and a square have same area. The ratio of the side of the square to the radius of the circle will be :
A√π:1B1:√πC1:πDπ:1
The diameter of a circle is equal to the side of the square. What is the area of the square if the area of the circle is 36 pi sq cm.
View SolutionAn equilateral triangle, a square and a circle have equal perimeters. If T denotes the area of triangle, S, the area of square and C, the area of the circle, then :
View SolutionThe areas of a circle and a square are same. The ratio of the side of the square to the radius of the circle is
View SolutionA square and a regular hexagon have equal perimeters. Their areas are in the ratio:
View SolutionThe area of square is 16π area of a circle. The ratio of the side of the square to the diameter of the circle is
View Solution
