A mass sliding down a slope without rotating gains which type of energy?
potential
kinetic
Rotational
Latent heat
The correct Answer is:B
Similar Questions
A thin hollow cylinder
slides without rotating with a speed v.
Find the ratio of kinetic energies in the two cases.View SolutionA hollow cylinder open at both ends slides without rotating, and then rolls without slipping with the same speed. The ratio of the kinetic energy in the two cases is (taken in order)
View Solution
Knowledge Check
- Question 1 - Select One
A person wishes to slide down a rope whose breaking load is 35 of the weight of the person Minimum acceleration by which the person should slide down without breaking the rope is:
A0.8gB1.2gC0.6gD0.4g - Question 2 - Select One
A block of mass m sliding down an inclined at constant speed is initial at a height h shown the ground as shown in the figure above . The coefficient of kinetic friction between the mass and the inclined is μ . If the mass constinues to slide down the inclined at a constant speed how much energy is displaced by friction by the time the mass reaches the bottom of the incline?
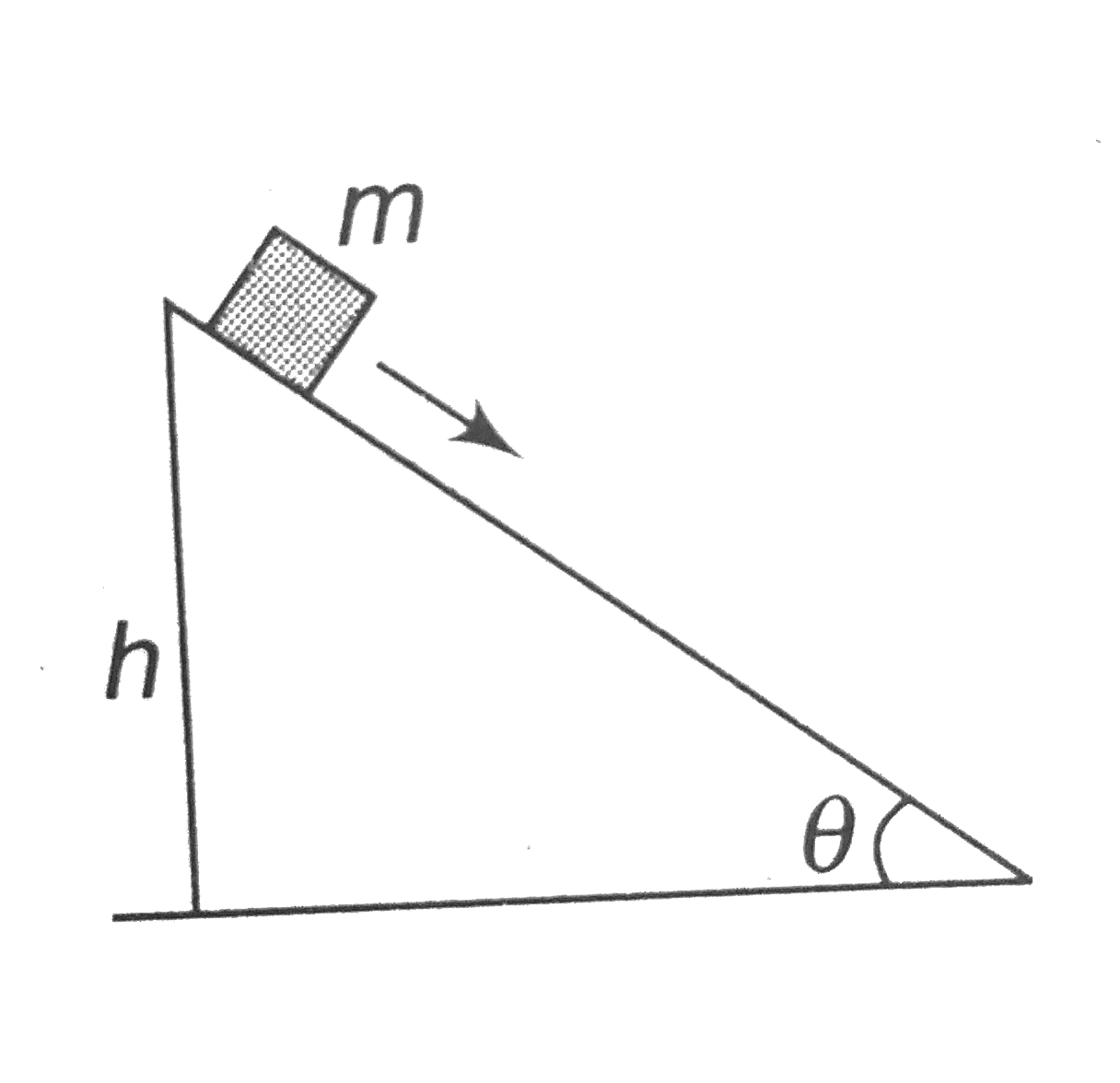 Amgh/θBmghCμmgh/sinθDmghsinθ
Amgh/θBmghCμmgh/sinθDmghsinθ - Question 3 - Select One
A small mass slide down an inclined plane of inclination theta with the horizontal. The coefficent of friction is μ=μ0 x where x is the distance through which the mass slide down and μ0,a contant. Then the speed is maxmum after the mass covers a distance of.
Acosθμ0Bsinθμ0Ctanθμ0D2tanθμ0
A hollow cylinder open at both ends slides without rotating, and then rolls without slipping with the same speed. The ratio of the kinetic energy in the two cases is (taken in order)
View SolutionA small mass slides down an inclined plane of inclination θ with the horizontal the coefficient of friction is μ=μ0x, where x is the distance through which the mass slides down. Then the distance covered by the mass before it stops is
View SolutionA small mass slides down an inclined plane of inclination θ with the horizontal. The co-efficient of friction is μ=μ0 x where x is the distance through which the mass slides down and μ0 a constant. Then, the distance covered by the mass before it stops is
View SolutionA small mass slides down an inclined plane of inclination θ with the horizontal. The co-efficient of friction is μ=μ0 x where x is the distance through which the mass slides down and μ0 a constant. Then, the distance covered by the mass before it stops is
View SolutionTwo blocks of mass 2m and m slide down the slope AB having same friction coefficient Then:
 View Solution
View Solution

